- КВАДРАТИЧНЫЙ ДИФФЕРЕНЦИАЛ
на римановой поверхности R - правило, которое каждому локальному параметру z, отображающему параметрич. окрестность
 в замкнутую комплексную
в замкнутую комплекснуюплоскость
 ставит в соответствие функцию Qz :
ставит в соответствие функцию Qz :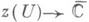 такую, что для всяких локальных параметров z1 :
такую, что для всяких локальных параметров z1 : и z2 :с
и z2 :с  непустым пересечением
непустым пересечением  в последнем выполнено соотношение
в последнем выполнено соотношение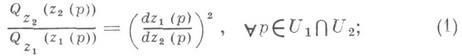
здесь z(U)- образ Uв
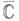 при отображении z. К. д. часто обозначается символом Q(z)dz2, к-рому приписывается указанная инвариантность относительно выбора локального параметра z. Иначе говоря, К. д.- это нелинейный дифференциал типа (2,0) на римановой поверхности.
при отображении z. К. д. часто обозначается символом Q(z)dz2, к-рому приписывается указанная инвариантность относительно выбора локального параметра z. Иначе говоря, К. д.- это нелинейный дифференциал типа (2,0) на римановой поверхности.Функции
 входящие в определение К. д., обычно предполагаются измеримыми или даже аналитическими. В последнем случае К. д. наз. аналитическим. Точка
входящие в определение К. д., обычно предполагаются измеримыми или даже аналитическими. В последнем случае К. д. наз. аналитическим. Точка  наз. нулем или полюсом порядка кдифференциала Q(z)dz2, если для каждого локального параметра z функция
наз. нулем или полюсом порядка кдифференциала Q(z)dz2, если для каждого локального параметра z функция  имеет в рсоответственно нуль или полюс порядка k. Нули и полюсы К. д. наз. его критическими точками. Нули и простые полюсы наз. конечными критич. точками, и их совокупность обозначают С. Множество всех полюсов порядка
имеет в рсоответственно нуль или полюс порядка k. Нули и полюсы К. д. наз. его критическими точками. Нули и простые полюсы наз. конечными критич. точками, и их совокупность обозначают С. Множество всех полюсов порядка 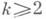 обозначают Н.
обозначают Н.Если кривая
 имеет в каждой своей точке qотносительно локального параметра zкасательную с направляющим вектором az(q). и
имеет в каждой своей точке qотносительно локального параметра zкасательную с направляющим вектором az(q). и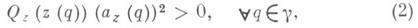
то К. д. Q(z)dz2 наз. положительным и пишут Q(z)dz2>0 на кривой у. Если в (2) вместо знака > имеет место знак <, то К. д. Q(z)dz2 отрицателен (Q(z)dz2<0) на кривой у. Всякая максимальная на Rрегулярная кривая, на к-рой Q(z)dz2>0 (либо Q(z)dz2<0), наз. траекторией дифференциала Q(z)dz2 (соответственно ортогональной траекторией).
К. д. Q(z)dz2, определенный на конечной римановой поверхности Л, принадлежит R, если край дR поверхности Rлибо пуст, либо состоит из конечного числа точек
 и дуг у, на каждой из к-рых дифференциал Q(z)dz2 регулярен и положителен пли отрицателен. Если к тому же край dR пуст или если дифференциал Q(z)dz2 на dR регулярен и положителен, то Q(z)dz2 наз. положительным К. д. на R. Метрика
и дуг у, на каждой из к-рых дифференциал Q(z)dz2 регулярен и положителен пли отрицателен. Если к тому же край dR пуст или если дифференциал Q(z)dz2 на dR регулярен и положителен, то Q(z)dz2 наз. положительным К. д. на R. Метрика  называемая Q-м етрикой, однозначна на й и инвариантна относительно выбора локального параметра z.
называемая Q-м етрикой, однозначна на й и инвариантна относительно выбора локального параметра z.В нек-рой окрестности Uлюбой точки
 функция
функция 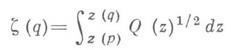 регулярна, однозначна и однолистна при каждом выборе знака подинтегрального выражения, причем всякая максимальная дуга траектории (или ортогональной траектории) из Uпри отображении Z(д)переходит в горизонтальный (соответственно вертикальный) прямолинейный интервал. Поэтому через каждую точку
регулярна, однозначна и однолистна при каждом выборе знака подинтегрального выражения, причем всякая максимальная дуга траектории (или ортогональной траектории) из Uпри отображении Z(д)переходит в горизонтальный (соответственно вертикальный) прямолинейный интервал. Поэтому через каждую точку  проходит траектория, являющаяся либо открытой дугой, либо жордановой кривой на R. Топологическая и конформная структуры семейства траекторий в малой окрестности всякой критпч. точки rполиостью классифицированы в зависимости от порядка критич. точки rи (если r- полюс 2-го порядка и z(r) = 0) от
проходит траектория, являющаяся либо открытой дугой, либо жордановой кривой на R. Топологическая и конформная структуры семейства траекторий в малой окрестности всякой критпч. точки rполиостью классифицированы в зависимости от порядка критич. точки rи (если r- полюс 2-го порядка и z(r) = 0) от  (см. Локальная структура траекторий). Описание глобальной структуры траекторий известно для конечных римановых поверхностей п имеет много важных приложений (см. также [1]).
(см. Локальная структура траекторий). Описание глобальной структуры траекторий известно для конечных римановых поверхностей п имеет много важных приложений (см. также [1]).О. Тайхмюллер (О. Teichmiiller) исследовал роль понятия К. д. для теории экстремальных конформных и квазиконформных отображений и для решения проблемы модулей римановых поверхностей (см. [1] - [3]). Он сформулировал принцип, согласно к-рому экстремальным задачам геометрич. теории функций ставятся в соответствие нек-рые К. д., причем каждому типу экстремальных задач соответствуют определенные особенности (полюсы) К. д., а геометрич. свойства решения связаны надлежащим образом со структурой траекторий К. д. В терминах К. д. доказаны неравенства для коэффициентов однолистных функций. Общее неравенство для коэффициентов, однолистных функций в семействах областей, расположенных на конечной римановой поверхности, носит название рбщей теоремы о коэффициентах и является конкретным воплощением принципа Тайхмюллера для широкого класса задач (см. [1], [4]). Принцип Тайхмюллера позволил также установить специальную теорему о коэффициентах и решить большое число конкретных экстремальных задач (см. [1], [5]).
Лит.:[1] Дженкинс Дж., Однолистные функции и конформные отображения, пер. с англ., М., 1962; [2] Шиффер М., Спенсер Д. К., Функционалы на конечных римановых поверхностях, пер. с англ., М., 1957; [3] Альфорс Л., Берс Л., Пространства римановых поверхностей и квазиконформные отображения, пер. с англ., М., 1961; [4] Тамразов П. М., "Матем. сб.", 1967, т. 72, № 1, с. 59-71; [5] Jenkins J. A., "III. J.Math.", 1964, v. 8, № 1, p. 80 - 99.
П. М. Тамразов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
