КОНЕЧНОМЕРНАЯ АССОЦИАТИВНАЯ АЛГЕБРА
- КОНЕЧНОМЕРНАЯ АССОЦИАТИВНАЯ АЛГЕБРА
- ассоциативное кольцо А, являющееся одновременно конечномерным векторным пространством над полем F, в к-ром выполняется следующее условие
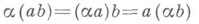
для всех 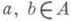 и
и  Размерность
Размерность 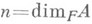 пространства Анад полем Fназ. размерностью алгебры Анад F. Принято также говорить, что алгебра Аявляется n-мерной. Всякая n-мерная ассоциативная алгебра Анад полем Fимеет точное представление матрицами порядка n+1 над F, т. е. существует изоморфизм алгебры Ана нек-рую подалгебру алгебры всех квадратных матриц порядка
пространства Анад полем Fназ. размерностью алгебры Анад F. Принято также говорить, что алгебра Аявляется n-мерной. Всякая n-мерная ассоциативная алгебра Анад полем Fимеет точное представление матрицами порядка n+1 над F, т. е. существует изоморфизм алгебры Ана нек-рую подалгебру алгебры всех квадратных матриц порядка  над F. Если, кроме того, алгебра Асодержит единицу, то она имеет точное представление матрицами порядка пнад F.
над F. Если, кроме того, алгебра Асодержит единицу, то она имеет точное представление матрицами порядка пнад F.
Пусть е г, . .. , е п- некоторый базис векторного пространства Анад F(он наз. также базисом алгебры А)и 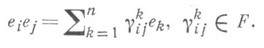
Элементы  поля Fназ. структурными константами алгебры Ав данном базисе. Они образуют тензор третьего ранга в пространстве А.
поля Fназ. структурными константами алгебры Ав данном базисе. Они образуют тензор третьего ранга в пространстве А.
Основные теоремы о К. а. а. Радикал: Джекобсона К. а. а. нильпотентен и, если основное поле сепарабельно, отщепляется полупрямым слагаемым (см. Веддерберна- Мальцева теорема). Полупростая К. а. а. над полем разлагается в прямую сумму магричных алгебр над телами. Если основное поле Fалгебраически замкнуто, то полупростая К. а. а. распадается в прямую сумму матричных алгебр над F. Простые конечномерные алгебры исчерпываются полными матричными алгебрами над телами (теорема Веддерберна). В частности, К. а. а. без делителей нуля оказывается телом. Над полем действительных чисел К. а. а. с делением (т. е. тела) исчерпываются следующими примерами: поле действительных чисел, поле комплексных чисел, тело кватернионов (теорема Фробениуса).
Многие из упомянутых структурных свойств К. а. а. имеют место и в более широких классах нётеровых и артиновых колец (см., напр., Веддерберна- Артина. теорема).
Лит.:[1] Ван дер Варден Б. Л., Алгебра, пер. с нем., М., 1976; [2] Аlbert A. A., Structure of algebras, N. Y., 1939.
В. <Н. <Латышев.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "КОНЕЧНОМЕРНАЯ АССОЦИАТИВНАЯ АЛГЕБРА" в других словарях:
Алгебра Хопфа — Алгебра Хопфа алгебра, являющаяся унитарной ассоциативной коалгеброй и, таким образом, биалгеброй c антигомоморфизмом специального вида. Названа в честь Х. Хопфа. Алгебры Хопфа встречаются в алгебраической топологии, где они возникли в… … Википедия
КЛИФФОРДА АЛГЕБРА — конечномерная ассоциативная алгебра над коммутативным кольцом, впервые рассмотренная У. Клиффордом (W. Clifford) в 1876. Пусть К коммутативное кольцо с единицей, Е свободный K модуль, Q квадратичная форма на Е. К. а. квадратичной формы Q(или пары … Математическая энциклопедия
АЛГЕБРА С ДЕЛЕНИЕМ — алгебра Анад полем F, для любых элементов и bк рой уравнения разрешимы в А. Ассоциативная А. с д., рассматриваемая как кольцо, является телом, а ее центр С полем и Если то А. с д. Аназ. центральной А. с д. Конечномерные центральные ассоциативные… … Математическая энциклопедия
ЛИ ГРАДУИРОВАННАЯ АЛГЕБРА — алгебра Ли над полем К, градуированная при помощи нек рой абелевой группы А, т. е. разложенная в прямую сумму подпространств , таким образом, что Если А упорядоченная группа, то для каждой фильтрованной алгебры Ли ассоциированная с ней… … Математическая энциклопедия
ЙОРДАНОВА АЛГЕБРА — алгебра, в к рой справедливы тождества 4 Такие алгебры впервые возникли в работе П. Йордана [1], посвященной аксиоматизации основ квантовой механики (см. также [2]), а затем нашли применения в алгебре, анализе и геометрии. Пусть А ассоциативная… … Математическая энциклопедия
СЕПАРАБЕЛЬНАЯ АЛГЕБРА — конечномерная полупростая ассоциативная алгебра Анад полем k, остающаяся полупростой при любом расширении Kполя k(т. е. алгебра полупроста для любого поля ). Алгебра Асепарабельна тогда и только тогда, когда центры простых компонент этой алгебры… … Математическая энциклопедия
ЛИ АЛГЕБРА — лиева алгебра, унитарный k модуль Lнад коммутативным кольцом k с единицей, к рый снабжен билинейным отображением прямого произведения в L, обладающим следующими двумя свойствами: 1) [ х, х] = 0 (откуда вытекает антикоммутативность 2) ( х,[ у,… … Математическая энциклопедия
ЦЕНТРАЛЬНАЯ ПРОСТАЯ АЛГЕБРА — простая ассоциативная алгебра с единицей, являющаяся центральной алгеброй. Всякая конечномерная Ц … Математическая энциклопедия
ЛИ p-АЛГЕБРА — ограниченная алгебра Ли, алгебра Lнад полем kхарактеристики р>0 (или, более общо, над кольцом простой характеристики р>0), снабженная р отображением таким, что выполняются следующие соотношения: Здесь внутреннее дифференцирование алгебры L … Математическая энциклопедия
РАДИКАЛЫ — колец и алгебр понятие, впервые возникшее в классической структурной теории конечномерных алгебр в нач. 20 в. Под Р. первоначально понимался наибольший нильпотентный идеал конечномерной ассоциативной алгебры. Алгебры с нулевым Р. (называемые… … Математическая энциклопедия
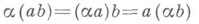
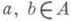 и
и  Размерность
Размерность 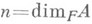 пространства Анад полем Fназ. размерностью алгебры Анад F. Принято также говорить, что алгебра Аявляется n-мерной. Всякая n-мерная ассоциативная алгебра Анад полем Fимеет точное представление матрицами порядка n+1 над F, т. е. существует изоморфизм алгебры Ана нек-рую подалгебру алгебры всех квадратных матриц порядка
пространства Анад полем Fназ. размерностью алгебры Анад F. Принято также говорить, что алгебра Аявляется n-мерной. Всякая n-мерная ассоциативная алгебра Анад полем Fимеет точное представление матрицами порядка n+1 над F, т. е. существует изоморфизм алгебры Ана нек-рую подалгебру алгебры всех квадратных матриц порядка  над F. Если, кроме того, алгебра Асодержит единицу, то она имеет точное представление матрицами порядка пнад F.
над F. Если, кроме того, алгебра Асодержит единицу, то она имеет точное представление матрицами порядка пнад F.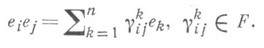
 поля Fназ. структурными константами алгебры Ав данном базисе. Они образуют тензор третьего ранга в пространстве А.
поля Fназ. структурными константами алгебры Ав данном базисе. Они образуют тензор третьего ранга в пространстве А.