- ЙОРДАНОВА АЛГЕБРА
- алгебра, в к-рой справедливы тождества
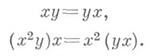 4
4Такие алгебры впервые возникли в работе П. Йордана [1], посвященной аксиоматизации основ квантовой механики (см. также [2]), а затем нашли применения в алгебре, анализе и геометрии.
Пусть А- ассоциативная алгебра над полем характеристики
 Множество Ас операциями сложения и йорданова умножения
Множество Ас операциями сложения и йорданова умножения
образует алгебру A(+), к-рая является йордановой. Й. а., изоморфная подалгебре алгебры А (+) для некрой ассоциативной алгебры А, наз. специальной. Роль специальных алгебр в теории Й. а. во многом аналогична роли ассоциативных алгебр в теории альтернативных алгебр. В основе этой аналогии лежит теорема о том, что всякая двупорожденная подалгебра Й. а. специальна. (Всякая двупорожденная подалгебра альтернативной алгебры - ассоциативна.) Однако класс специальных Й. а. не является многообразием, т. е. не задается тождествами, поскольку специальные алгебры могут иметь неспециальные гомоморфные образы. Тем не менее, найден ряд тождеств 8-й и 9-й степеней, которым удовлетворяет всякая специальная Й. а. и не удовлетворяют нек-рые неспециальные алгебры, а также доказано, что таких тождеств степени <7 не существует. Необходимое и достаточное условие специальности алгебры: Й. а. специальна тогда и только тогда, когда она изоморфно вложима в Й. а., каждое счетное подмножество к-рой лежит в подалгебре, порожденной двумя элементами.
Примеры. 1) Пусть V- векторное пространство над полем Fс симметрической билинейной формой f(х, у),a F-e0+V- пространство на единицу большей размерности, на к-ром формулой

 определяется умножение.' Возникающая таким образом алгебра наз. алгеброй симметрической билинейной формы f. Она изоморфно вкладывается в алгебру C(V, f)(+), где С(V, f) - алгебра Клиффорда формы f, и потому является специальной Й. а.
определяется умножение.' Возникающая таким образом алгебра наз. алгеброй симметрической билинейной формы f. Она изоморфно вкладывается в алгебру C(V, f)(+), где С(V, f) - алгебра Клиффорда формы f, и потому является специальной Й. а.2) Пусть А - ассоциативная алгебра и f - ее инволюция (антиизоморфизм порядка два). Множество

является подалгеброй в A(+) и образует специальную Й. а.
3) Пусть С- альтернативная неассоциативная алгебра над полем Fс инволюцией
 неподвижные элементы к-рой лежат в ассоциативном центре алгебры С. В алгебре матриц С 3 третьего порядка над Сподмножество
неподвижные элементы к-рой лежат в ассоциативном центре алгебры С. В алгебре матриц С 3 третьего порядка над Сподмножество
где
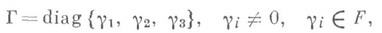
относительно операций сложения и йорданова умножения образует неспецлальную Й. а. Такая алгебра не является гомоморфным образом никакой специальной алгебры.
Конечномерные простые Й. а. над алгебраически замкнутым полем Fхарактеристики
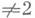 полностью классифицированы (см. [3]). Центральные простые конечномерные Й. а. разбиваются на пять серий. Серии (А) - (D) бесконечны и состоят из специальных алгебр, серия (Е) состоит из одной неспециальной алгебры:
полностью классифицированы (см. [3]). Центральные простые конечномерные Й. а. разбиваются на пять серий. Серии (А) - (D) бесконечны и состоят из специальных алгебр, серия (Е) состоит из одной неспециальной алгебры:(А) Fn(+);
(В) H(Fn,J1), где J1 :
 (С) H(F2n, JS),где JS :
(С) H(F2n, JS),где JS : S=diag {Q,Q,...,Q}, Q=
S=diag {Q,Q,...,Q}, Q=
(D) F-e0+V - алгебра симметрической невырожденной билинейной формы;
(Е) H(С 3, J1), где С - алгебра Кэли - Диксона со стандартной инволюцией. Эта алгебра 27-мерна над F.
Во всякой конечномерной Й. а. J радикал (наибольший нильидеал) Nнильпотентен и факторалгебра
 есть конечная прямая сумма простых Й. а. Если факторалгебра
есть конечная прямая сумма простых Й. а. Если факторалгебра  сепарабельна, то алгебра J обладает разложением J=N+W в сумму радикала и полупростой подалгебры W, изоморфной J. В случае поля характеристики 0 все полупростые слагаемые Wсопряжены относительно автоморфизмов специального вида (см. [3]). С некоторыми ограничениями на алгебру это верно и в случае поля характеристики р>0.
сепарабельна, то алгебра J обладает разложением J=N+W в сумму радикала и полупростой подалгебры W, изоморфной J. В случае поля характеристики 0 все полупростые слагаемые Wсопряжены относительно автоморфизмов специального вида (см. [3]). С некоторыми ограничениями на алгебру это верно и в случае поля характеристики р>0.Обобщением теории конечномерных Й. а. является теория Й. а. с условием минимальности для квадратичных (внутренних) идеалов (см. [3], [4], [5]). Квадратичный идеал"Q алгебры J - это такое подпространство, что
 для всех
для всех  и
и  где {abc}=( аb) с+(bс )а-( са)b- тройное йорданово произведение. Если J - Й. а. с условием минимальности для квадратичных идеалов и R - ее квазирегулярный радикал, то факторалгебра J/R есть конечная прямая сумма простых алгебр, к-рые описаны за исключением Й. а. с делением. В случае, когда алгебра J специальна, доказано, что радикал Rнильпотентен и конечномерен.
где {abc}=( аb) с+(bс )а-( са)b- тройное йорданово произведение. Если J - Й. а. с условием минимальности для квадратичных идеалов и R - ее квазирегулярный радикал, то факторалгебра J/R есть конечная прямая сумма простых алгебр, к-рые описаны за исключением Й. а. с делением. В случае, когда алгебра J специальна, доказано, что радикал Rнильпотентен и конечномерен.Алгебраическая специальная Й. а., удовлетворяющая нетривиальному (для специальных алгебр) тождеству, локально конечномерна; специальная йорданова нильалгебра с нетривиальным тождеством локально нильпотентна [6]. В частности, специальная алгебраическая (ниль) Й. а. ограниченного индекса является локально конечномерной (нильпотентной). Конечно порожденная разрешимая И. а. нильпотентна, в общем случае это не верно даже для специальных алгебр.
Йорданово Ф-операторное кольцо, являющееся конечно порожденным Ф-модулем с нильпотентными порождающими элементами, нильпотентно [7].
Каждой Й. а. можно различными способами сопоставлять алгебры Ли (см. [3], [8]). Ряд теорем о Й. а. получен с помощью известных теорем об алгебрах Ли. Так, напр., доказано, что полупростая конечномерная Й. а. над алгебраически замкнутым полем характеристики О имеет базис с целочисленными структурными константами. Для теории алгебр Ли эти конструкции также полезны, так как с их помощью реализуются нек-рые важные классы алгебр Ли. Напр., алгебра Ли дифференцирований простой Й. а. типа (Е) есть исключительная простая алгебра Ли F4, а алгебра линейных преобразований этой же алгебры, оставляющих инвариантной нек-рую кубич. форму, есть исключительная простая алгебра Ли Е е. При помощи другой конструкции, сопоставляющей альтернативной алгебре степени 2 и
Й. а. степени 3 некоторую алгебру Ли, можно реализовать все пять простых исключительных алгебр Ли типов G2, F4, Е 6, Е 7, Е 8.
Интересно, наконец, отметить, что нек-рые алгебры, возникающие в генетике, являются йордановыми [10].
Лит.:[1] Jordan P., "Nachr. Akad. Wiss. Gottingen. Math.-Phys. Kl. 2A", 1933, S. 209-17; [2] Эмх Ж., Алгебраические методы в статистической механике и квантовой теории поля, пер. с англ., М., 1976; [3] Jacobson N., Structure and representations of Jordan algebras, Providence, 1968; [4] Me Crimmon K., "Prof. Nat. Acad. Sci USA", 1969, v. 02, №3, p. 671 - 78; [5] Слинько А. М., "Алгебра и логика", 1972, т. 11, № 6, с. 711-24; [6] Ширшов А. И., "Матем. сб.", 1957, т. 41, № 3, с. 381-94; [7] Шестаков И. П., "Алгебра и логика", 1971, т. 10, № 4, с. 407-48; [8] Sсhafer R. D., An introduction to nonassociative algebras, N.Y., 1966; [9] Gоrdоn S. R., "J. of Algebra", 1973, v. 24, p. 258-82; [10] Sсhafer R. D., "Amer. J. Math.", 1949, v. 71, p. 121-35; [11] Коесher M., An elementary approach to bounded symmetric domains, Houston, 1969; [12]Слинько А. М. и др., Йордановы алгебры, в. 1, Новосиб., 1976.
А. М. Слинько.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
