АЛГЕБРА С ДЕЛЕНИЕМ

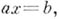
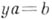- алгебра Анад полем F, для любых элементов и bк-рой уравнения разрешимы в А. Ассоциативная А. с д., рассматриваемая как кольцо, является телом, а ее центр С - полем и Если то А. с д. Аназ. центральной А. с д. Конечномерные центральные ассоциативные А. с д. над F, рассматриваемые с точностью до изоморфизма, можно отождествить с элементами Браузра группы поля F. Пусть обозначает размерность Анад F. Если - максимальное подполе в А . Согласно Фробениуса теореме, все ассоциативные конечномерные А. с д. над полем действительных чисел Rисчерпываются самим R, полем комплексных чисел и алгеброй кватернионов. Поэтому группа В(R).является циклической порядка 2. При отказе от ассоциативности появляется еще один пример А. с д. над полем действительных чисел - Кэли - Диксона алгебра. Эта алгебра альтернативна и имеет размерность 8 над R. Если А - конечномерная (не обязательно ассоциативная) А. с д. над R, то [А:R] имеет одно из следующих значений: 1, 2, 4, 8.

Лит.:[1] Курош А. Г., Лекции по общей алгебре, 2 изд., М., 1973; [2] А1bert A. A., Structure of algebras, 3 ed., Providence, [1968]; [3] Херстейн И., Некоммутативные кольца, пер. с англ., М., 1972; [4] Адамс Дж. Ф., "Математика", 1961, т. 5, № 4, с. 3-86. Е. Н. Кузьмин.