КОМПЛЕКСИФИКАЦИЯ АЛГЕБРЫ ЛИ
- КОМПЛЕКСИФИКАЦИЯ АЛГЕБРЫ ЛИ
 над R - комплексная алгебра Ли
над R - комплексная алгебра Ли  являющаяся тен зорным произведением алгебры
являющаяся тен зорным произведением алгебры  на поле комплексных чисел С над полем действительных чисел R:
на поле комплексных чисел С над полем действительных чисел R:
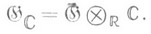
Таким образом, К. а. Ли  получается из
получается из  расширением поля скаляров с R до С. Элементами алгебры
расширением поля скаляров с R до С. Элементами алгебры  можно считать пары (u, v), и,
можно считать пары (u, v), и, тогда операции в
тогда операции в
 будут определяться формулами:
будут определяться формулами:

Алгебра  наз. также комплексной оболочкой алгебры Ли
наз. также комплексной оболочкой алгебры Ли 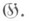
Нек-рые важные свойства алгебр наследуются при комплексификации:  нильпотентна, разрешима или полупроста тогда и только тогда, когда
нильпотентна, разрешима или полупроста тогда и только тогда, когда  обладает этим свойством. Однако простота
обладает этим свойством. Однако простота  не влечет, вообще говоря, простоту
не влечет, вообще говоря, простоту 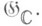
Понятие К. а. Ли тесно связано с понятием вещественной формы комплексной алгебры Ли. Вещественная подалгебра Ли f в комплексной алгебре Ли  наз. вещественной формой алгебры Ли
наз. вещественной формой алгебры Ли  если всякий элемент
если всякий элемент  однозначно представим в виде x=u+iv, где и,
однозначно представим в виде x=u+iv, где и,  К. а. Ли f естественно изоморфна алгебре I). Не всякая комплексная алгебра Ли имеет вещественную форму. С другой стороны, заданная комплексная алгебра Ли, вообще, может иметь несколько неизоморфных вещественных форм. Так, алгебра Ли всех вещественных матриц порядка пи алгебра Ли всех антиэрмитовых матриц порядка пявляются неизоморфными вещественными формами алгебры Ли всех комплексных матриц порядка п(у к-рой имеются и другие вещественные формы).
К. а. Ли f естественно изоморфна алгебре I). Не всякая комплексная алгебра Ли имеет вещественную форму. С другой стороны, заданная комплексная алгебра Ли, вообще, может иметь несколько неизоморфных вещественных форм. Так, алгебра Ли всех вещественных матриц порядка пи алгебра Ли всех антиэрмитовых матриц порядка пявляются неизоморфными вещественными формами алгебры Ли всех комплексных матриц порядка п(у к-рой имеются и другие вещественные формы).
Лит.:[1] Наймарк М. А., Теория представлений групп, М., 1976; [2] Желобенко Д. П., Компактные группы Ли и их представления, М., 1970; [3] Гантмахер Ф., "Матем. сб.", 1939, т. 5, в. 2, с. 217-50.
В. Л. Попов.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "КОМПЛЕКСИФИКАЦИЯ АЛГЕБРЫ ЛИ" в других словарях:
КОМПЛЕКСИФИКАЦИЯ ГРУППЫ ЛИ — G над R комплексная группа Ли G С, содержащая Gв качестве вещественной подгруппы Ли и такая, что алгебра Ли группы Gявляется вещественной формой алгебры Ли группы (см. Комплексификация ал гебра Ли). Группа Gпри этом наз. вещественной формой… … Математическая энциклопедия
СЖАТИЕ — алгебры Ли, стягивание алгебры Ли, операция, противоположная деформации алгебры Ли. Пусть конечномерная вещественная алгебра Ли, набор ее структурных констант в фиксированном базисе е 1, . . ., е n и А (t), , кривая в группе невырожденных… … Математическая энциклопедия
БЕСКОНЕЧНОМЕРНОЕ ПРЕДСТАВЛЕНИЕ — группы Ли представление группы Ли в бесконечномерном векторном пространстве. Теория представлений групп Ли есть часть общей теории, представлений то пологич. групп. Специфика групп Ли позволяет использовать в этой теории средства анализа (в… … Математическая энциклопедия
КИЛЛИНГА ФОРМА — билинейная форма специального вида на конечномерной алгебре Ли, введенная В. Киллингом [1]. Пусть конечномерная алгебра Ли над полем k. К. ф. на алгебре наз. билинейная форма где tr обозначает след линейного оператора, a ad x образ хпри… … Математическая энциклопедия
ИВАСАВЫ РАЗЛОЖЕНИЕ — однозначное представление любого элемента gнекомпактной связной полупростой вещественной группы Ли Gв виде произведения g= кап элементов k, а, п аналитич. подгрупп К, А, N группы Gсоответственно, где подгруппы К, А, N определяются следующим… … Математическая энциклопедия
ОРБИТ МЕТОД — метод изучения унитарных представлений групп Ли. С помощью О. м. была построена теория унитарных представлений нильпотентных групп Ли, а также указана возможность его применения к другим группам [1]. О. м. основан на следующем экспериментальном… … Математическая энциклопедия
ЛИ КОМПАКТНАЯ ГРУППА — компактная группа, являющаяся конечномерной вещественной группой Ли. Ли к. г. могут быть охарактеризованы как конечномерные локально связные компактные топологич. группы. Если G0 связная компонента единицы Ли к. г. С, то группа связных компонент… … Математическая энциклопедия
ВЕЙЛЯ ГРУППА — 1) В. г. симметрий корневой системы. В зависимости от конкретной реализации корневой системы рассматривают п различные В. г.; так возникают В. г. полупростой расщепляемой алгебры Ли, В. г. симметрич. пространства, В. г. алгебраич. группы. Пусть… … Математическая энциклопедия
ОДНОРОДНЫЙ ВЫПУКЛЫЙ КОНУС — открытый строго выпуклый конус Vв векторном пространстве Rn, однородный относительно группы линейных преобразований таких, что (автоморфизмов конуса V). О. в. к. и наз. изоморфными, если существует изоморфизм объемлющих векторных пространств,… … Математическая энциклопедия
КОС ТЕОРИЯ — раздел топологии и алгебры, изучающий косы и группы, составленные из их классов эквивалентности, и различные обобщения этих групп [1]. Коса из пнитей объект, состоящий из двух параллельных плоскостей Р 0 и Р 1 в трехмерном пространстве R3,… … Математическая энциклопедия
 над R - комплексная алгебра Ли
над R - комплексная алгебра Ли  являющаяся тен зорным произведением алгебры
являющаяся тен зорным произведением алгебры  на поле комплексных чисел С над полем действительных чисел R:
на поле комплексных чисел С над полем действительных чисел R: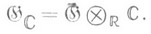
 получается из
получается из  расширением поля скаляров с R до С. Элементами алгебры
расширением поля скаляров с R до С. Элементами алгебры  можно считать пары (u, v), и,
можно считать пары (u, v), и, тогда операции в
тогда операции в будут определяться формулами:
будут определяться формулами:
 наз. также комплексной оболочкой алгебры Ли
наз. также комплексной оболочкой алгебры Ли 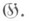
 нильпотентна, разрешима или полупроста тогда и только тогда, когда
нильпотентна, разрешима или полупроста тогда и только тогда, когда  обладает этим свойством. Однако простота
обладает этим свойством. Однако простота  не влечет, вообще говоря, простоту
не влечет, вообще говоря, простоту 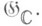
 наз. вещественной формой алгебры Ли
наз. вещественной формой алгебры Ли  если всякий элемент
если всякий элемент  однозначно представим в виде x=u+iv, где и,
однозначно представим в виде x=u+iv, где и,  К. а. Ли f естественно изоморфна алгебре I). Не всякая комплексная алгебра Ли имеет вещественную форму. С другой стороны, заданная комплексная алгебра Ли, вообще, может иметь несколько неизоморфных вещественных форм. Так, алгебра Ли всех вещественных матриц порядка пи алгебра Ли всех антиэрмитовых матриц порядка пявляются неизоморфными вещественными формами алгебры Ли всех комплексных матриц порядка п(у к-рой имеются и другие вещественные формы).
К. а. Ли f естественно изоморфна алгебре I). Не всякая комплексная алгебра Ли имеет вещественную форму. С другой стороны, заданная комплексная алгебра Ли, вообще, может иметь несколько неизоморфных вещественных форм. Так, алгебра Ли всех вещественных матриц порядка пи алгебра Ли всех антиэрмитовых матриц порядка пявляются неизоморфными вещественными формами алгебры Ли всех комплексных матриц порядка п(у к-рой имеются и другие вещественные формы).