КОМПЛЕКС

прямых - множество К прямых в трехмерном пространстве (проективном, аффинном, евклидовом), зависящее от трех параметров. Прямая lО K наз. лучом К. Через каждую точку Мпространства проходит однопараметрическая совокупность лучей К.- конус К _М. К. определяет соответствие между точками луча К. и плоскостями, проходящими через этот луч: каждой точке Млуча lсоответствует плоскость П, касательная к конусу К _М в точке М. Такое соответствие наз. нормальной корреляцией. В каждой плоскости пространства располагается однопараметрическое семейство лучей К., огибающих плоскую кривую s. Инфлекционным центром луча 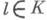наз. точка в к-рой кривая s плоскости П, соответствующей точке Мв нормальной корреляции, имеет возврат. На каждом луче К. имеется в общем случае четыре инфлекционных центра. Точкой прикосновения линейчатой поверхности К. наз. такая точка Мна ее образующей, в к-рой касательная плоскость поверхности совпадает с плоскостью П, соответствующей точке Мв нормальной корреляции. На каждой образующей линейчатой поверхности К. имеется в общем случае две и только две точки прикосновения. Линии, описанные этими точками, наз. линиями прикосновения линейчатой поверхности. Главными поверхностями К. наз. линейчатые поверхности, у к-рых линии прикосновения суть их асимптотич. линии. Проективную классификацию К. можно осуществлять по кратности инфлекционных центров их лучей.

В евклидовом пространстве на каждом луче lопределяется инвариантная точка С(центр луча), в к-рой вектор нормали к плоскости П, соответствующей в нормальной корреляции точке С, ортогонален нормали к плоскости П, соответствующей несобственной точке луча l. Примеры К.: специальный К.- множество всех касательных к данной поверхности; линейный К., задаваемый линейным однородным уравнением относительно грассмановых координат луча К.; специальный линейный К.- множество прямых трехмерного пространства, пересекающих данную прямую.

Наряду с К. прямых рассматривают К. (трехпараметрич. семейства) плоскостей, коник, квадрик и других фигур (см. Фигур многообразие).

Лит.:[1] Фиников С. П., Теория конгруэнции, М.- Л., 1950; [2] Кованцов Н. И., Теория комплексов, К., 1963.

В. С. Малаховский.