ОРБИТ МЕТОД

- метод изучения унитарных представлений групп Ли. С помощью О. м. была построена теория унитарных представлений нильпотентных групп Ли, а также указана возможность его применения к другим группам [1].

О. м. основан на следующем "экспериментальном" факте: существует глубокая связь между унитарными неприводимыми представлениями группы Ли G и орбитами этой группы в коприсоединенном представлении. Решение основных задач теории представлений с помощью О. м. осуществляется следующим образом (cм. [2]).

I. Конструкция и классификация неприводимых унитарных представлений. Пусть W - орбита действительной группы Ли G в коприсоединенном представлении, F - точка этой орбиты (являющаяся линейным функционалом на алгебре Лп 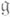группы G), G(F) - стабилизатор точки F, 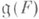-алгебра Ли группы G(F). Поляризацией точки Fназ. комплексная подалгебра 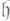в ,

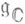где 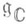- комплексификация алгебры Ли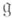, обладающая свойствами:

1)

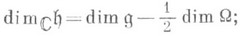
2) содержится в ядре функционала Fна ;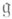

3) 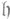инвариантна относительно Ad G(F).

Пусть 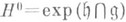и H=G(F)^.H⁰. Поляризация 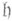наз. действительной, если , и чисто комплексной, если 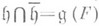. Функционал Fопределяет характер (одномерное унитарное представление) 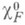группы 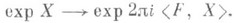Н ⁰ по формуле

Пусть продолжается до характера 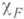группы H.

Если - действительная поляризация, то пусть

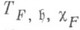- индуцированное характером X_F подгруппы H представление группы G(см. Индуцированное представление). Если - чисто комплексная поляризация, то пусть 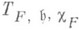- голоморфно индуцированное представление, действующее в пространстве голоморфных функций на G/H.

Первая основная гипотеза состоит в том, что представление неприводимо и его класс эквивалентности зависит 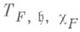только от орбиты W. и от выбора продолжения 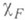характера . Эта гипотеза доказана для нильпотентных групп [1] и для разрешимых групп Ли [5]. Для нек-рых орбит простой особой группы G₂ гипотеза неверна [7]. Возможность продолжения и степень его неоднозначности зависят от топологич. свойств орбиты: препятствием к продолжению служат двумерные когомологии орбиты, а в качестве параметра, нумерующего различные продолжения, можно взять одномерные когомологии орбиты. Более точно, пусть B_W - каноническая 2-форма на орбите W. Для существования продолжения необходимо и достаточно, чтобы форма B_W. принадлежала целочисленному классу (т. е. интеграл ее по любому двумерному циклу был целым числом); если это условие выполнено, то множество продолжений параметризуется характерами фундаментальной группы орбиты.

Вторая основная гипотеза состоит в том, что указанным способом получаются все унитарные неприводимые представления рассматриваемой группы G. Единственным (1983) противоречащим этой гипотезе примером являются т. н. дополнительные серии представлений полупростых групп Ли.

II. Функториальные свойства соответствия между орбитами и представлениями. Значительное место в теории представлений занимают вопросы о разложении на неприводимые компоненты представления, получаемого ограничением на подгруппу Ннеприводимого представления группы G и индуцированием с помощью неприводимого представления подгруппы . О. м. дает ответ на эти вопросы в терминах естественной проекции ( означает переход к сопряженному пространству; проекция рсостоит в ограничении функционала с 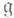на 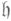). А именно, пусть G - экспоненциальная группа Ли (для таких групп соответствие между орбитами и представлениями взаимно однозначно).

Тогда неприводимое представление группы G, соответствующее орбите , при ограничении на Нразлагается на неприводимые компоненты, соответствующие тем орбитам 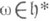, к-рые лежат в р(W), а представление группы G, индуцированное неприводимым представлением группы Н, соответствующим орбите , разлагается на неприводимые компоненты, соответствующие тем орбитам , к-рые имеют непустое пересечение с прообразом р ^-1(w). Из этих результатов вытекают два следствия: если неприводимые представления T_i соответствуют орбитам W_i, i=l, 2, то тензорное произведение разлагается на неприводимые компоненты, соответствующие тем орбитам W, к-рые лежат в арифметич. сумме W₁+W₂, квазирегулярное представление группы G в пространстве функций на G/H разлагается на неприводимые компоненты, соответствующие тем орбитам 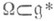, для к-рых образ 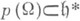содержит нуль.

III. Теория характеров. Для характеров неприводимых представлений (как обобщенных функций на группе) предложена [2] следующая универсальная формула:

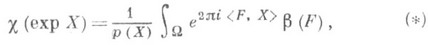
где 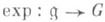- экспоненциальное отображение алгебры Ли 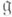в группу G, р(X) - квадратный корень из плотности инвариантной меры Хаара на G в канонич. координатах, b - форма объема на орбите W, связанная с канонической 2-формой В _W. соотношением b=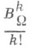, 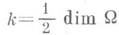. Эта формула справедлива для нильпотентных групп, разрешимых групп типа 1, компактных групп, дискретной серии представлений полупростых действительных групп и основной серии представлений комплексных полупростых групп. Для нек-рых вырожденных серий представлений SL(3, 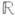) формула неверна. Из формулы 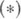полудается простая формула для вычисления инфинитезимального характера неприводимого представления T_W, соответствующего орбите W, а именно: каждому оператору Лапласа D на G может быть сопоставлен 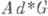-инвариантный многочлен P_D на 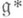так, что значение инфинптезимального характера представления T_W. на элементе D в точности равно значению Р _D на W.

IV. Конструкцию неприводимого унитарного представления группы G по ее орбите W в коприсоеди-ненном представлении можно рассматривать как операцию квантования нек-рой гамильтоновой системы, для к-рой W играет роль фазового пространства, a G - роль многомерного некоммутативного времени (или группы симметрии). При этом G-орбиты в коприсоединенном представлении - это все G-однородные симплектич. многообразия, допускающие квантование. Таким образом, вторую основную гипотезу можно переформулировать так: каждая элементарная квантовая система с временем (или группой симметрии) G получается квантованием из соответствующей классич. системы (см. [2]).

Обнаружена также связь О. м. с теорией вполне интегрируемых гамильтоновых систем (см. [11]).

Лит.:[1] Кириллов А. А., "Успехи матем. наук", 1962, т. 17, в. 4, с. 57-110; [2] его же, Элементы теории представлений, 2 изд., М., 1978; [3] Диксмье Ж., Универсальные обертывающие алгебры, пер. с франц., М., 1978; [4] Simms D. J., Woodhouse N. M. J. , Lectures on geometric guantizatiori, В.- Hdlb.- N. Y., 1976; [5] Auslander L., Коstant В., "Invent, math.", 1971. v. 14, p. 255-354; [6] Moore C.C. "Ann. Math.", 1965, v. 82, .№ 1, p. 146 - 82; [7] Rothschild L. P., Wоlf J. A., "Arm. Sci. Ecole norm, super. Ser.4",1974, v. 7, № 2, p. 155-74; [8] Representations des groupcs de Lie resolubles, P., 1972; [91 Г и н з б у р г В. А., "Докл. АН СССР", 1979, т. 249, № 3, с. 525-28; [10] Кirillоv A. A., Infinite dimensional groups, their representations, orbits, invariants, в сб.: Proc. Int. Congr. Math., Helsinki, 1978; [11] Rеуman A. G.,Sernenov-Tian-Shansky M. A., "Invent, math.", 1979, v. 54, № 1, p. 81 - 100. А. А. Кириллов.