Внешняя мера — В математике, в частности в теории меры, внешняя мера это функция, определенная на всех подмножествах данного множества с действительным значением, что удовлетворяет нескольким дополнительным техническим условиям. Общая теория внешней меры… … Википедия
Теорема Каратеодори о продолжении меры — В теории меры теорема Каратеодори утверждает, что произвольная (счётно аддитивная) мера на некотором кольце подмножеств множества может быть продлена на σ кольцо, порожденное кольцом . В случае σ конечности меры такое продолжение является… … Википедия
ВНЕШНЯЯ МЕРА — неотрицательная функция множества, обозначаемая , заданная на счетно аддитивном классе множеств, содержащем вместе с множеством любое его подмножество и обладающая свойствами: монотонности, т. е. счетной полуаддитивности, т. е. , где пустое… … Математическая энциклопедия
ФУНКЦИЙ ТЕОРИЯ — раздел математики, занимающийся изучением свойств различных функций. Теория функций распадается на две области: теорию функций действительного переменного и теорию функций комплексного переменного, различие между которыми настолько велико, что… … Энциклопедия Кольера
ПУАНКАРЕ ТЕОРЕМА ВОЗВРАЩЕНИЯ — одна из основных теорем общей теории динамич. систем с инвариантной мерой. Пусть движение системы описывается дифференциальными уравнениями (1) где однозначные функции Xi( х 1, . . ., х п).удовлетворяют условию так что уравнения (1) допускают… … Математическая энциклопедия
МАРТИНА ГРАНИЦА — в теории потенциала идеальная граница Грина пространстваW (см. также Кольцевая граница), позволяющая построить характеристич. представление положительных гар монич. функций на W. Пусть W локально компактное, но не компактное топологич.… … Математическая энциклопедия
ПОЛУНЕПРЕРЫВНАЯ ФУНКЦИЯ — функция из первого Бэра класса. Подробнее, числовая функция f, определенная на полном метрич. пространстве X, наз. полунепрерывной снизу (сверху) в точке , если Функция f наз. полунепрерывной снизу (сверху) на X, если она. полунепрерывна снизу… … Математическая энциклопедия
Борель, Эмиль — У этого термина существуют и другие значения, см. Борель. Феликс Эдуард Жустин Эмиль Борель Félix Edouard Justin Émile Borel … Википедия
Борель Э. — Эмиль Борель Феликс Эдуард Жустин Эмиль Борель (фр. Félix Edouard Justin Émile Borel) (7 января 1871 3 февраля 1956, Париж) французский математик и политический деятель. Биография Эмиль Борель родился на юге Франции, близ Авиньона. Его отец,… … Википедия
Борель Эмиль — Эмиль Борель Феликс Эдуард Жустин Эмиль Борель (фр. Félix Edouard Justin Émile Borel) (7 января 1871 3 февраля 1956, Париж) французский математик и политический деятель. Биография Эмиль Борель родился на юге Франции, близ Авиньона. Его отец,… … Википедия
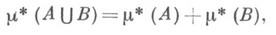
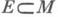принадлежит области определения р., т. е. m*-измеримо, тогда и только тогда, когда
(здесь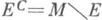 
); если Еm*-измеримо, то m(E) =m*(E). Область определения К. м. содержит все борелевские множества. Если m* - внешняя мера в классе всех подмножеств метрич. пространства такая, что всякое открытое множество m*-измеримо, то m* - внешняя К. м.