- КАРАТЕОДОРИ КЛАСС
- класс Сфункций
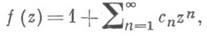
регулярных в круге |z|<1 и имеющих в нем положительную действительную часть. Класс назван по имени К. Каратеодори, определившего точное множество значений системы коэффициентов{c1, с2, . .., с п},
на классе С(см. [1], [2]).Теорема Рисса - Герглотца. Для того чтобы функция f(z) принадлежала классу С, необходимо и достаточно, чтобы она допускала представление интегралом Стилтьеса
где m(t) - функция, неубывающая на отрезке [-p,p]и такая, что m(p)-m( -p)=1.
С помощью этого представления легко выводятся интегральные параметрич. представления для классов функций, выпуклых и однолистных в круге, звездообразных и однолистных в круге и др.
Теорема Каратеодори - Теплица. Множество значений системы {с 1, с 2,..., с п},
на классе Сесть замкнутое выпуклое ограниченное множество К п точек n-мерного комплексного евклидова пространства, в к-рых определители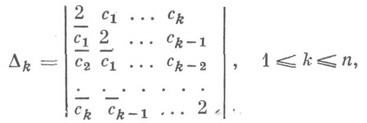
либо все положительны, либо положительны до какого-то номера, начиная с к-рого все равны нулю. В последнем случае получается поверхность П n тела К п. Каждой точке П n отвечает только одна функция класса Си она имеет вид
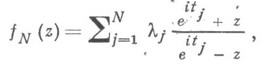
где
при j
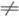k, k, j = 1, . . ., N.Множество значений коэффициента с п, п=1,2, ..., на классе Сесть круг
окружности |с n| = 2 соответствуют только функции
Множество значений f(z0) (z0 фиксировано, |z0|<l) на классе Сесть круг, диаметром к-рого является отрезок
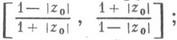границе этого круга соответствуют только функции
Рассматривались множества значений систем функционалов и более общего вида (см. [6]). Для класса Сполучены вариационные формулы, с помощью к-рых показано, что ряд экстремальных задач в классе Срешается функциями fN(z),
(см. [В]).Основной подкласс С - класс С r функций
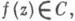имеющих действительные коэффициенты с n, n=1, 2, .... Для того чтобы функция f(z)принадлежала классу С r, необходимо и достаточно, чтобы она допускала представление 
где m(t)- функция, неубывающая на [0, 2p], m(2p)- -m(0)=l. С помощью этого представления решаются многие экстремальные задачи на классе С г.
Лит.:[1] Саratheоdоrу С, "Math. Ann.", 1907, Bd 64, S. 95-115; [2] его же, "Rend. Circolo mat. Palermo", 1911, v. 32, p. 193-217; [3] Tоeplitz О., там же, р. 191 - 92; [4] Ricsz P., "Ann. scient. Ecole norm, super.", 1911, t. 28, p. 33-62; [5] Herglotz G., "Ber. Verhandl. Sachsisch. Akad. Wiss. Leipzig. Math.-naturwiss. Kl.", 1911, Bd 63, S. 501 - 11; [6] Голузин Г. М., Геометрическая теория функций комплексного переменного, 2 изд., М., 1966.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
