- ИЗОМЕТРИЧЕСКОЕ ПОГРУЖЕНИЕ
- погружение k-мерного метрич. многообразия М к в n-мерное риманово пространство V,
 в виде k-мерной поверхности
в виде k-мерной поверхностиФ, при к-ром расстояние между любыми двумя точками на М k совпадает с расстоянием между их образами, измеренным по поверхности Ф в пространстве Vn. Это определение можно обобщить, если риманово пространство заменить более общим метрич. пространством. Частным случаем И. п. является изометрическое вложение - взаимно однозначное погружение.
Основными вопросами теории И. п. являются; 1) проблема возможности И. п. данного многообразия в данное пространство; 2) в случае существования И. п.- проблема его единственности. Эти проблемы рассматриваются при различных условиях на многообразие и его изометрич. образ - гладкости, регулярности, аналитичности, выпуклости и т. д. При каждом из перечисленных условий конкретизация основных вопросов теории И. п. производится в следующих аспектах: а) вопрос глобального И. п. М k в Vn;б) вопрос локального И. п. М k в Vn (отыскание И. п. в Vдостаточно малой окрестности отмеченной точки
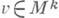 ); в) в локальном и глобальном случаях отыскание минимального ртакого, что М k погружаемо в евклидово пространство Е k+p размерности k+р (число рназ. классом погружения многообразия М k);г) вопросы изгибания И. п.
); в) в локальном и глобальном случаях отыскание минимального ртакого, что М k погружаемо в евклидово пространство Е k+p размерности k+р (число рназ. классом погружения многообразия М k);г) вопросы изгибания И. п.С аналитич. точки зрения задача нахождения И. п. М k в Vn равносильна решению системы нелинейных уравнений с частными производными. Для И. п. в Е п эта система имеет вид:
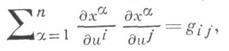
где x={xa(us)} - искомое И. п., gij -метрический тензор многообразия М k в локальных координатах и 1, . . ., и k. При решении этой системы в глобальном случае используются так наз. свободные отображения хв Е n (см. Нэша теорема о неявной функции). В локальных аналитич. адачах место теоремы о неявной функции занимает Коши - Ковалевской теорема. Роль свободного отображения и теоремы о неявной функции сохраняется и в общем случае для погружений класса С r,
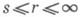 , r=a, в римановы и псевдоримановы пространства. И. п. класса С 1 используют иные методы, основанные на деформации погружения, позволяющей менять погружения и следить за изменением метрики. При исследованиях И. п. в Е п используется также система уравнений Гаусса - Петерсона - Кодацци.
, r=a, в римановы и псевдоримановы пространства. И. п. класса С 1 используют иные методы, основанные на деформации погружения, позволяющей менять погружения и следить за изменением метрики. При исследованиях И. п. в Е п используется также система уравнений Гаусса - Петерсона - Кодацци.Глобальные изометрические погружения. Всякое компактное риманово многообразие М k класса С(
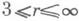 )допускает изометрич. вложение класса С в любой шар пространства Е п, где п
)допускает изометрич. вложение класса С в любой шар пространства Е п, где п  (3k2+11k)/2; если М k некомпактно, то оно допускает вложение класса
(3k2+11k)/2; если М k некомпактно, то оно допускает вложение класса  в любую часть пространства Е n, где
в любую часть пространства Е n, где 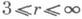 и п
и п 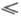 (3k2+11k) (k+l)/2 (см. [6]). Размерность пространства Е п снижается в случаях r=
(3k2+11k) (k+l)/2 (см. [6]). Размерность пространства Е п снижается в случаях r=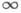 и r=а:всякое риманово многообразие Mk (компактное или нет, с краем или без края) класса С( С а )допускает изометрич. вложение класса
и r=а:всякое риманово многообразие Mk (компактное или нет, с краем или без края) класса С( С а )допускает изометрич. вложение класса 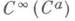 в Е п, где
в Е п, где 
Для k-мерного гиперболич. пространства (k>2) получено в явном виде изометрич. вложение класса С в Е 6k-5, а для k-мерного эллиптич. пространства (k>2) - изометрич. вложение класса Св Е п, п=k(k+3)/2.
В перечисленных результатах гладкость поверхности Ф не выше, чем гладкость погружаемой метрики. Этот факт не является случайным: именно, всякая k-мерная (
 ) поверхность Ф класса
) поверхность Ф класса 
 в Е п является И. п. класса С- а нек-рого риманова многообразия М к класса С> а (см. [8]).
в Е п является И. п. класса С- а нек-рого риманова многообразия М к класса С> а (см. [8]).Нижняя граница для размерности пространства Е п, в к-рое можно осуществить И. п. риманова многообразия, дается теоремой: пусть компактное риманово многообразие М к класса С 4 обладает следующим свойством: в каждой точке М к существует q-плоскость такая, что в ней все кривизны по всем двумерным направлениям неположительны; тогда М к не допускает И. п. класса С 4 в любое Е" с
 если условие, наложенное на кривизну многообразия М к, распространяется на одну точку и д=п, то существует И. п. класса С 4 в Е'2к~2. Так, напр., плоский ^-мерный тор не допускает И. п. класса С 4 в E2k-1; если k - степень двойки, то действительное проективное пространство RPk, снабженное метрикой со всюду положительной скалярной кривизной, в частности k-мерное эллиптич. пространство, не допускает изометрич. вложения класса С 2 в Е 2k.
если условие, наложенное на кривизну многообразия М к, распространяется на одну точку и д=п, то существует И. п. класса С 4 в Е'2к~2. Так, напр., плоский ^-мерный тор не допускает И. п. класса С 4 в E2k-1; если k - степень двойки, то действительное проективное пространство RPk, снабженное метрикой со всюду положительной скалярной кривизной, в частности k-мерное эллиптич. пространство, не допускает изометрич. вложения класса С 2 в Е 2k.продолжение Изометрическое погружение...
Результаты, относящиеся к И. п. класса С 1, резко отличаются от предыдущих. Они формулируются в следующем виде: если компактное риманово многообразие М k класса С 0 (с границей или без нее) допускает погружение класса С 1 в Е п при
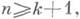 то оно также допускает И. п. класса С 1 в Е п;если некомпактное риманово многообразие М к класса С 0 допускает короткое погружение (т. е. не удлиняющее в каждой точке линейный элемент) класса С 1 в Е п,
то оно также допускает И. п. класса С 1 в Е п;если некомпактное риманово многообразие М к класса С 0 допускает короткое погружение (т. е. не удлиняющее в каждой точке линейный элемент) класса С 1 в Е п,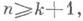 не пересекающее свое предельное множество, то оно допускает также И. п. класса С 1 в Е n (см. [7]) (здесь предельное множество погружения многообразия М k в Е n есть совокупность точек хпространства Е п, для каждой из к-рых в М k существует расходящаяся последовательность, образ к-рой сходится в Е п к х). В частности, любое компактное риманово многообразие М k класса С 0 (с границей или без нее) допускает И. п. класса С 1 в Е 2k;любое некомпактное риманово многообразие класса С 0 допускает И. п. класса С 1 в E2k+1.
не пересекающее свое предельное множество, то оно допускает также И. п. класса С 1 в Е n (см. [7]) (здесь предельное множество погружения многообразия М k в Е n есть совокупность точек хпространства Е п, для каждой из к-рых в М k существует расходящаяся последовательность, образ к-рой сходится в Е п к х). В частности, любое компактное риманово многообразие М k класса С 0 (с границей или без нее) допускает И. п. класса С 1 в Е 2k;любое некомпактное риманово многообразие класса С 0 допускает И. п. класса С 1 в E2k+1.Если И. п. (изометрич. вложения) класса С 1 риманова многообразия М k в Е п с n>k можно соединить короткой регулярной гомотопией (короткой диффеотопией), то их можно соединить изгибанием, составленным из И. п. (изометрич. вложений) класса С 1. В частности, в компактном случае И. п. (изометрич. вложения) класса С 1 тогда и только тогда можно соединить изгибанием, составленным из И. п. (изометрич. вложений) класса С 1, когда они регулярно гомотопны (диффеотопны).
Локальные изометрические погружения. В 1873 Л. Шлефли (L. Schlafli) высказал гипотезу, согласно к-рой всякое риманово многообразие размерности кдопускает локальное И. п. в евклидово пространство Е n, где п=k(k+1)/2. Эта гипотеза доказана лишь для аналитич. многообразий (см. Жане теорема);более того, во всяком римановом многообразии М k класса С а с отмеченной точкой существует окрестность отмеченной точки, допускающая изометрич. вложение класса Св Е п, п=k(k+1)/2. В римановом пространстве М k класса С с отмеченной точкой существует окрестность отмеченной точки, допускающая изометрич. вложение класса С°° в Е n, где n = k(k+1)/2+k (см. [7]). С другой стороны, у всякого риманова многообразия класса С 0 с отмеченной точкой существует окрестность ее, допускающая изометрич. вложение класса С 1 в Ek+1.
Несколько иное направление составляет отыскание условий, при к-рых данное многообразие Мимеет *И. п. в Е n, где n<k(k+1)/2. Это связано с тем, что не всякое риманово многообразие М k допускает И. п. в Е n:при
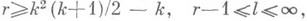 множество римановых метрик, локально индуцируемых на гладком многообразии М k с. отмеченной точкой локальными вложениями класса С в Е n, п<k(k+1)/2, нигде не плотно во множестве всех римановых метрик класса С l на М k, снабженном обычной С l -топологией; при r=2 и
множество римановых метрик, локально индуцируемых на гладком многообразии М k с. отмеченной точкой локальными вложениями класса С в Е n, п<k(k+1)/2, нигде не плотно во множестве всех римановых метрик класса С l на М k, снабженном обычной С l -топологией; при r=2 и  утверждение остается верным, если n и kсвязаны неравенством
утверждение остается верным, если n и kсвязаны неравенством 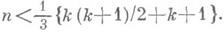
При решении задачи об определении класса (см. выше) И. п. многообразия минимальное р, найденное в локальной постановке, оценивает снизу значение ри для глобального И. п. Однако точное значение наименьшего р, при к-ром любое многообразие М k, k>2, класса С r,
 допускает И. п. класса С r в Е k+ Р, неизвестно. Имеются нек-рые частные приемы вычисления класса И. п. данного риманова многообразия М k в пространство Е п. Так, р=0 в том и только в том случае, если тензор кривизны многообразия М k тождественно равен нулю. Существует алгебраич. критерий, позволяющий установить, будет ли класс И. п. данного многообразия равен 1, и основанный на том факте, что для метрик класса 1 при нек-рых дополнительных условиях уравнения Петерсона - Кодацци являются следствием уравнений Гаусса [И]. В частности, метрики постоянной положительной кривизны имеют класс 1 и реализуются при k>3 в виде гиперсфер евклидова пространства. Но если Риччи кривизна для М k равна нулю, то
допускает И. п. класса С r в Е k+ Р, неизвестно. Имеются нек-рые частные приемы вычисления класса И. п. данного риманова многообразия М k в пространство Е п. Так, р=0 в том и только в том случае, если тензор кривизны многообразия М k тождественно равен нулю. Существует алгебраич. критерий, позволяющий установить, будет ли класс И. п. данного многообразия равен 1, и основанный на том факте, что для метрик класса 1 при нек-рых дополнительных условиях уравнения Петерсона - Кодацци являются следствием уравнений Гаусса [И]. В частности, метрики постоянной положительной кривизны имеют класс 1 и реализуются при k>3 в виде гиперсфер евклидова пространства. Но если Риччи кривизна для М k равна нулю, то 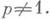
Почти все изложенные результаты обобщаются на И. п. одного риманова пространства в другое. Так, напр., обстоит дело с погружениями класса С 1, с локальными И. п., с достаточно гладкими И. п. k-мерных многообразий в Vn большой размерности, со связями между порядками гладкости поверхности и ее метрики и т. д.
Задачи И. п. переносятся на псевдоримановы многообразия. В этом случае кроме размерностей ки пучитываются размерности k+ и k-=k-k+ положительной и отрицательной части метрич. тензора на погружаемом многообразии М k и соответствующие размерности п + и n_ = n-п + объемлющего пространства V". Так, теорема Жане сохраняется в псевдоримановом случае при
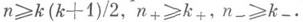
Изометрические погружения двумерных многообразий. Многие задачи этого типа получили законченное решение в том смысле, что пространство, в к-ром строится погружение, имеет минимальную размерность. Здесь разработаны специальные методы решения, основанные на о. <бщей теории нелинейных дифференциальных уравнений с частными производными и топологогеометрич. соображениях.
Вейля проблема, поставленная в 1916, гласит: допускает ли двумерное риманово многообразие М 2 И. п. в Е 3, если оно гомеоморфно сфере и имеет положительную гауссову кривизну? Полное решение проблемы Вейля, обобщенной в том смысле, что речь идет об И. п. М 2 в трехмерное риманово пространство V3, дано А. В. Погореловым [3]: пусть V3- полное трехмерное риманово пространство, М 2+- замкнутое гомеоморфное сфере риманово многообразие с гауссовой кривизной, всюду большей нек-рой постоянной k0 (большей, меньшей или равной нулю); тогда, если кривизна пространства всюду меньше k0, то M2+ допускает И. п. в виде регулярной поверхности Ф. Это погружение можно осуществить так, чтобы данный двумерный элемент aмногообразия Mk (точка и пучок направлений в ней) совпал бы с данным изометричным адвумерным элементом а' в пространстве V3, и поверхность располагалась бы по заданную сторону от. <площадки элемента a'. Если метрика пространства V3 и многообразия М 2+ принадлежат классу С,
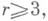 то поверхность Ф принадлежит по крайней мере классу Cr-1,v, 0<v<l. Поверхность двумерным элементом определяется однозначно. Любые два И. п. класса С,
то поверхность Ф принадлежит по крайней мере классу Cr-1,v, 0<v<l. Поверхность двумерным элементом определяется однозначно. Любые два И. п. класса С,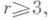 r=а, в V3 можно соединить изгибанием, составленным из И. п. того же класса.
r=а, в V3 можно соединить изгибанием, составленным из И. п. того же класса.С совершенно иной точки зрения проблема Вейля исследована А. Д. Александровым, к-рый построил теорию (нерегулярных) двумерных многообразий с выпуклой метрикой[4] (такие многообразия можно определить путем предельного перехода от регулярных многообразий с положительной гауссовой кривизной) и наметил следующий план решения проблемы Вейля: 1) обобщить постановку проблемы, беря в качестве М 2 многообразие с произвольной, вообще говоря, нерегулярной выпуклой метрикой; 2) затем установить регулярность И. п. в зависимости от регулярности метрики М 2. Осуществление (им же) первой части этого плана привело к исчерпывающему результату: всякое гомеоморфное сфере многообразие с выпуклой метрикой допускает И. п. в Е 3 в виде замкнутой выпуклой поверхности. Реализация второй части плана, проведена А. В. Погореловым в [3], где полностью решен вопрос о регулярности выпуклой поверхности с регулярной метрикой: если выпуклая поверхность
 имеет метрику класса С k, a,
имеет метрику класса С k, a, 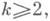 0<a<1, и положительную гауссову кривизну, то Ф принадлежит классу Ck, a. Если метрика поверхности Ф - аналитическая, то и поверхность Ф - аналитическая. Сходные теоремы имеют место для выпуклых поверхностей в пространстве постоянной кривизны. При определенных условиях существуют И. п. двумерных римановых многообразий положительной гауссовой кривизны, гомеоморфных плоскости или кругу. Наряду с этим построены примеры аналитич. метрик положительной кривизны, заданных в круге и не допускающих И. п. класса С 2 в Е 3.
0<a<1, и положительную гауссову кривизну, то Ф принадлежит классу Ck, a. Если метрика поверхности Ф - аналитическая, то и поверхность Ф - аналитическая. Сходные теоремы имеют место для выпуклых поверхностей в пространстве постоянной кривизны. При определенных условиях существуют И. п. двумерных римановых многообразий положительной гауссовой кривизны, гомеоморфных плоскости или кругу. Наряду с этим построены примеры аналитич. метрик положительной кривизны, заданных в круге и не допускающих И. п. класса С 2 в Е 3.Теорема Гильберта о непогружаемости класса С 2 в Е 3 плоскости Лобачевского естественно привела к вопросу, погружаются ли в Е 3 какие-либо полные двумерные метрики с кривизной, ограниченной сверху отрицательной константой (так наз. метрики типа L)? Решение этой проблемы дано Н. В. Ефимовым [14]: если Ф - полная поверхность класса С 2 в Е 3 с гауссовой кривизной К(х), то
 так что, в частности, метрики типа А не допускают И. п. в Е 3. В связи с этой теоремой представляет интерес вопрос о том, какие части метрик типа А (т. е. области двумерного многообразия, на к-ром задается двумерная метрика) могут быть погружены в Е 3. Определенный ответ на этот вопрос получен в [15]. Пусть в бесконечной полосе
так что, в частности, метрики типа А не допускают И. п. в Е 3. В связи с этой теоремой представляет интерес вопрос о том, какие части метрик типа А (т. е. области двумерного многообразия, на к-ром задается двумерная метрика) могут быть погружены в Е 3. Определенный ответ на этот вопрос получен в [15]. Пусть в бесконечной полосе 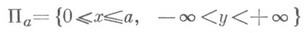 плоскости Е 2 с декартовыми координатами х, у задана форма ds2=dx2+B2(x, у) dy2, причем функция
плоскости Е 2 с декартовыми координатами х, у задана форма ds2=dx2+B2(x, у) dy2, причем функция 
 и обладает следующими свойствами: а) она сама, все ее производные до г-го порядка, а также константы Липшица по удля производных по уот производных (r-1)-го порядка ограничены в П a; б) inf B>0; в) гауссова кривизна
и обладает следующими свойствами: а) она сама, все ее производные до г-го порядка, а также константы Липшица по удля производных по уот производных (r-1)-го порядка ограничены в П a; б) inf B>0; в) гауссова кривизна  Тогда форма ds2 порождает на многообразии с краем П а риманову структуру класса С r,1, и полученное риманово многообразие допускает И. п. класса С r,1,
Тогда форма ds2 порождает на многообразии с краем П а риманову структуру класса С r,1, и полученное риманово многообразие допускает И. п. класса С r,1, 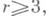 в Е 3. В частности, существует И. п. любого геодезич. круга с произвольной (регулярной) метрикой отрицательной кривизны. Имеется ряд теорем об И. п. в Е 3 некомпактных частей метрик отрицательной кривизны [5]. Даны также оценки размеров области, на к-рую однозначно проектируется поверхность отрицательной (и отделенной от нуля) кривизны.
в Е 3. В частности, существует И. п. любого геодезич. круга с произвольной (регулярной) метрикой отрицательной кривизны. Имеется ряд теорем об И. п. в Е 3 некомпактных частей метрик отрицательной кривизны [5]. Даны также оценки размеров области, на к-рую однозначно проектируется поверхность отрицательной (и отделенной от нуля) кривизны.Так как метрики типа А в целом в Е 3 не погружаются, то ставится вопрос об И. п. этих метрик в евклидовы пространства больших размерностей. В этом направлении имеются лишь частные результаты; так, напр., существует изометрич. вложение класса С°° плоскости Лобачевского в E6 и И. п. в Е 5;дан пример регулярной метрики типа Л, допускающей И. п. в E4; неизвестно, однако, допускает ли плоскость Лобачевского И. п. класса С,
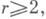 в Е 4.
в Е 4.Вопрос И. п. в Е 3 метрик знакопеременной кривизны остается открытым даже в случае локальной проблемы. Так, напр., построен [16] пример двумерного риманова многообразия класса С 2, 1, не допускающего локального И. п. класса С 2, 1 в Е 3. Вместе с тем задача о реализации аналитич. метрик знакопеременной кривизны решается следующей теоремой [17]: пусть в прямоугольнике
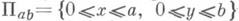 плоскости Е 2 задана метрика ds2=dx2+В 2( х, у)dy2 и пусть В( х, у)- аналитич. функция в нек-ром открытом прямоугольнике, содержащем П а, b; тогда аналитическое риманово многообразие с краем, порожденное на П аb, заданной метрикой, допускает аналитич. И. п. в Е 3. Имеется ряд результатов, касающихся И. п. регулярных метрик знакопеременной кривизны в евклидово пространство более высокой (но близкой к трем) размерности. Так, если М 2- полное риманово многообразие класса С 3,a, гомеоморфное плоскости, то любая его компактная часть допускает И. п. класса С 2, a в E4; гомеоморфное тору риманово многообразие также допускает И. п. в Е 4. Всякое компактное двумерное риманово многообразие класса
плоскости Е 2 задана метрика ds2=dx2+В 2( х, у)dy2 и пусть В( х, у)- аналитич. функция в нек-ром открытом прямоугольнике, содержащем П а, b; тогда аналитическое риманово многообразие с краем, порожденное на П аb, заданной метрикой, допускает аналитич. И. п. в Е 3. Имеется ряд результатов, касающихся И. п. регулярных метрик знакопеременной кривизны в евклидово пространство более высокой (но близкой к трем) размерности. Так, если М 2- полное риманово многообразие класса С 3,a, гомеоморфное плоскости, то любая его компактная часть допускает И. п. класса С 2, a в E4; гомеоморфное тору риманово многообразие также допускает И. п. в Е 4. Всякое компактное двумерное риманово многообразие класса  допускает И. п. (и даже вложение) класса С ( С a )в Е 10, а если оно не имеет замкнутых компонент, то - в Е 9. Двумерная сфера с произвольной римановой метрикой класса
допускает И. п. (и даже вложение) класса С ( С a )в Е 10, а если оно не имеет замкнутых компонент, то - в Е 9. Двумерная сфера с произвольной римановой метрикой класса  допускает И. п. класса
допускает И. п. класса  в E7. а поверхность Клейна и лист Мёбиуса - И. п. в Е 4.
в E7. а поверхность Клейна и лист Мёбиуса - И. п. в Е 4.Если отказаться от регулярности погружения, то всякая двумерная риманова метрика класса С r,
 допускает И. п. класса С 1 в Е 3. Однако при этом будут нарушены обычные связи между внутренней и внешней геометрией поверхности, реализующей метрику. Построено локальное И. п. метрики двумерной сферы в виде локально невыпуклой поверхности в Е 3 класса С 1-01 при любом
допускает И. п. класса С 1 в Е 3. Однако при этом будут нарушены обычные связи между внутренней и внешней геометрией поверхности, реализующей метрику. Построено локальное И. п. метрики двумерной сферы в виде локально невыпуклой поверхности в Е 3 класса С 1-01 при любом 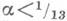 и аналогичное И. п. в целом при
и аналогичное И. п. в целом при  С другой стороны, если поверхность Ф принадлежит классу С 1, a,
С другой стороны, если поверхность Ф принадлежит классу С 1, a, то поверхность Ф, имеющая знакопостоянную внутреннюю кривизну, будет иметь ограниченную внешнюю кривизну. В частности, если внутренняя кривизна Ф положительна, то Ф будет локально выпуклой поверхностью, и если сверх того метрика поверхности регулярна, то регулярна и сама поверхность. Таким образом, нижняя грань значений а, при к-рых сохраняются связи между внутренней и внешней геометрией поверхности Ф класса С 1,a со знакопостоянной внутренней кривизной, принадлежит отрезку
то поверхность Ф, имеющая знакопостоянную внутреннюю кривизну, будет иметь ограниченную внешнюю кривизну. В частности, если внутренняя кривизна Ф положительна, то Ф будет локально выпуклой поверхностью, и если сверх того метрика поверхности регулярна, то регулярна и сама поверхность. Таким образом, нижняя грань значений а, при к-рых сохраняются связи между внутренней и внешней геометрией поверхности Ф класса С 1,a со знакопостоянной внутренней кривизной, принадлежит отрезку 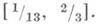 Наконец, все ориентируемые многообразия ограниченной внешней кривизны, не имеющие точек с кривизной 2p, допускают изометрич. вложения в Е 3 в виде дифференцируемых поверхностей. При исследовании нерегулярных И. п. изучались также кусочно линейные И. п. кусочно линейных метрик: так, всякая развертка, гомеоморфная замкнутой области на ориентируемой замкнутой поверхности, может быть изометрич. вложена в Е 3 в виде многогранника.
Наконец, все ориентируемые многообразия ограниченной внешней кривизны, не имеющие точек с кривизной 2p, допускают изометрич. вложения в Е 3 в виде дифференцируемых поверхностей. При исследовании нерегулярных И. п. изучались также кусочно линейные И. п. кусочно линейных метрик: так, всякая развертка, гомеоморфная замкнутой области на ориентируемой замкнутой поверхности, может быть изометрич. вложена в Е 3 в виде многогранника.Лит.:[1] Ефимов Н. В., в кн.: Тр. 4 Всесоюзного математического съезда, т. 1, Л., 1963, с. 86-99; [2] Бакельман И. Я., Вернер А. Л., Кантор Б. Е., Введение в дифференциальную геометрию "в целом", М., 1973; [3] Погорелов А. В., Внешняя геометрия выпуклых поверхностей, М., 1969; [4] Александров А. Д., Внутренняя геометрия выпуклых поверхностей, М.--Л., 1948: [5] Позняк Э. Г., Шикин Е. В., в сб.: Итоги науки и техники. Алгебра. Топология. Геометрия, т. 12, М., 1974, с. 171-207; [6] Нэш Дж., "Успехи матем. наук", 1971, т. 36, в. 4, с. 173-216; [7] Громов М. Л., Рохлин В. А., там же, 1970, т. 25, в. 5, с. 3-62; [8] Сабитов И. X., Шефель С. 3., "Сиб. матем. ж.", 1976, т. 17, № 4, с. 916-25; [9] Otsuki Т., "J. Math. Soc. Japan", 1954, v. 6, p. 221 - 34; [10] Нэш Дж., "Математика", 1957, т. 1, № 2, с. 3-16; [11] Розенсон Н. А., "Изв. АН СССР. Сер. Матем.", 1943, т. 7, с. 253-84; [12] Friedman A., "J. Math., Mech.", 1961, v. 10, p. 625-49; [13] Сабитов И. X., "Сиб. матем. ж.", 1976, т. 17,. № 4, с. 907-15; [14] Ефимов Н. В., "Матем. сб.", 1964, т. 64, Xs2, с. 286-320; [15] IIозняк Э. Г., "Укр. геометр. Сб.", 1966, в. 3, с. 78-92; [16] Погорелов А. В., "Докл. АН СССР", 1971, т. 198, №1, с. 42 - 43; [17] Позняк Э. Г., "Успехи матем. наук", 1973, т. 28, в. 4, с. 47-76; [18] Бураго Ю. Д., Залгаллер В. А., "Вестн. Ленингр. ун-та. Сер. матем., мехаш и астрон.", 1960, т. 7, №2, с. 66-80.
В. Т. Фоменко.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
