ГОМОЛОГИЧЕСКАЯ РАЗМЕРНОСТЬ

числовая характеристика объекта категории относительно некоторого выделенного класса объектов этой категории. Основная область применения этого понятия - категории модулей над кольцом.

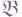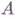Пусть - фиксированный класс объектов абелевой категории и объект из 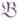, тогда (проективной) гомологической размерностью объекта Аотносительно класса 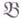наз. наименьшее число n, для к-рого существует точная последовательность вида

где все 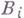из Если такого и не существует, то говорят, что Г. р. равна .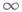

Пусть 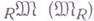- категория левых (правых) модулей над ассоциативным кольцом Rс единицей. Тогда:

а) если 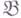- класс всех проективных левых R-модулей, то соответствующая Г. р. модуля Аназ. проективной размерностью и обозначается ;

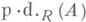б) если - класс всех плоских левых A-модулей, то соответствующая Г. р. модуля Аназ. слабой размерностью и обозначается 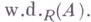Если - категория левых градуированных модулей над градуированным кольцом , а - класс всех левых проективных градуированных R-модулей, то соответствующая Г. р. градуированного R-модуля Аназ. градуированной проективной размерностью и обозначается .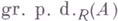

Рассматривается также двойственная конструкция. Если 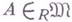, то наименьшее число птакое, что существует точная последовательность

где все модули 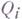инъективны, наз. инъективной размерностью модуля Аи обозначается

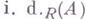
Пусть 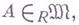тогда следующие условия равносильны:

а)

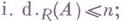
б) 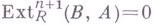для всех (см. ФункторExt);

б') 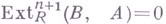для всех циклических модулей В;

в) - точный функтор относительно аргумента В;

г) если

- точная последовательность п модул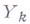и при ннъективны, то - инъективный модуль.

Эквивалентны между собой также условия:

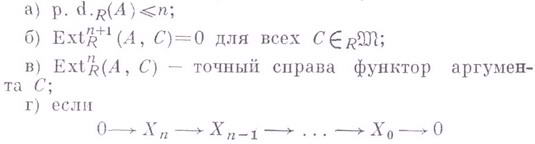
- точная последовательность и модул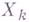и при проективны, то и - проективный модуль. Если последовательность

- точна, где и

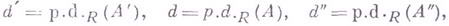
то

Если

Число

наз. левой глобальной размерностью кольца R.

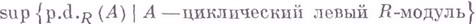
Если кольцо R обладает композиционным рядом левых идеалов, то

Число

наз. слабой глобальной размерностью кольца R, при этом

Число

наз. левой ограниченной глобальной размерностью кольца R.

Сюда же примыкают следующие размерности: если R - алгебра над коммутативным кольцом К, то проективная размерность R-бимодуля R (т. е. левого -модуля, где R^0p -противоположное R кольцо) наз. биразмерностью алгебры R и обозначается bid R; если G - группа, К - коммутативное кольцо, то (ко) гомологической размерностью группы Gназ. плоская (проективная) размерность модуля Кнад групповым кольцом KG c тривиальным действием группы Gна Ки обозначается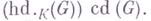

Ряд хорошо известных теорем можно переформулировать в терминах Г. р. Напр., теорема Веддерберна - Артина будет иметь вид: кольцо R классически полупросто тогда и только тогда, когда 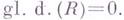Кольцо R регулярно (в смысле Неймана) тогда и только тогда, когда Равенство 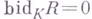для алгебры R над полем Кравносильно ее сепарабельности над К. Утверждение о том, что подгруппа свободной абелевой группы свободна, эквивалентно тому, что - кольцо целых чисел. Кольцо R, для к-рого 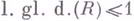наз. наследственным слева кольцом.

Левая и правая глобальные размерности кольца Rмогут не совпадать. Если же Rнётерово слева и справа, то

Если - гомоморфизм колец, то любой S-модуль 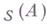можно рассматривать и как R-модуль, при этом:

Если кольцо R - фильтрованное, то

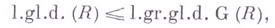
где - ассоциированное градуированное кольцо. В ряде случаев изучение Г. р. связано с мощностью рассматриваемых модулей. Это позволяет, в частности, оценивать разность между слабой и проективной размерностями модуля, а также разность между левой и правой глобальными размерностями кольца. Континуум-гипотеза равносильна утверждению о том, что

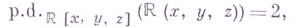
где - поле действительных чисел, - поле рациональных функций, а - кольцо многочленов над R.

Большая часть исследований по Г. р. посвящена выявлению связей Г. р. с другими характеристиками модулей и колец. Так, Гильберта теорема о сизигиях утверждает, что

где К - поле, а - кольцо многочленов от переменных х ₁, ..., х _п над К. К настоящему времени эта теорема значительно обобщена. Г. р. групповых алгебр разрешимых групп тесно связана с длиной разрешимого ряда группы и рангами ее факторов. Из равенства следует, что G- свободная группа (теорема Столлингса). Исследуются связи между Г. р. и другими размерностями модулей и колец. Напр., размерность по Круллю коммутативного кольца Rсовпадает с 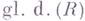тогда и только тогда, когда все локализации кольца Rпо простым идеалам имеют конечную размерность Крулля. Всякое коммутативное нётерово кольцо R, для которого 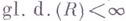, раскладывается в конечную прямую сумму областей целостности. Локальное кольцо регулярной точки наз. в алгебраич. геометрии локальным регулярным кольцом. Глобальная размерность такого кольца совпадает с его размерностью Крулля, а также с минимальным числом образующих его максимального идеала (регулярные локальные кольца являются областями целостности с однозначным разложением на простые множители, они остаются регулярными при локализациях по простым идеалам).

Лит.: [1] Картан А., Эйленберг С., Гомологическая алгебра, пер. с англ., М., 1960; [2] Оsofsky В. L., Homological dimensions ol modules, Providence, 1973.

В. Е. Говоров, А. В. Михалев.