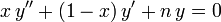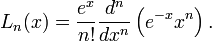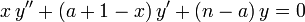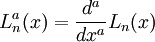Обобщённые полиномы Лагерра
- Обобщённые полиномы Лагерра
-
В математике, Многочлены Лагерра, названные в честь Эдмонда Лагерра (1834—1886), являются каноническими решениями Уравнения Лагерра:
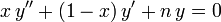
являющегося линейным дифференциальным уравнением второго порядка. Это уравнение имеет несингулярное решение только в случае, когда n неотрицательно.
Многочлены Лагерра, обычно обозначающиеся как 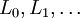 , являются последовательностью полиномов, которая может быть найдена по Формуле Родригеса
, являются последовательностью полиномов, которая может быть найдена по Формуле Родригеса
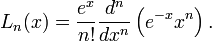
Несколько первых многочленов
В следующей таблице приведены несколько первых многочленов Лагерра:
Обобщённые полиномы Лагерра
Обобщённые полиномы Лагерра имеют вид:
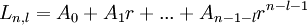
где:
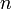 — главное (орбитальное) квантовое число;
— главное (орбитальное) квантовое число;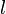 — орбитальное (азимутальное) квантовое число.
— орбитальное (азимутальное) квантовое число.
Обобщённые полиномы Лагерра 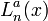 являются решениями уравнения:
являются решениями уравнения:
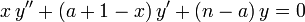
так что 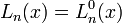 .
.
Обобщённые полиномы Лагерра могут быть выражены через полиномы Лагерра по формуле:
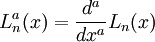
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Обобщённые полиномы Лагерра" в других словарях:
Полиномы Лагерра — В математике, Многочлены Лагерра, названные в честь Эдмонда Лагерра (1834 1886), являются каноническими решениями Уравнения Лагерра: являющегося линейным дифференциальным уравнением второго порядка. Это уравнение имеет несингулярное решение… … Википедия
Обобщенные полиномы Лагерра — В математике, Многочлены Лагерра, названные в честь Эдмонда Лагерра (1834 1886), являются каноническими решениями Уравнения Лагерра: являющегося линейным дифференциальным уравнением второго порядка. Это уравнение имеет несингулярное решение… … Википедия
Лагерра полиномы — В математике, Многочлены Лагерра, названные в честь Эдмонда Лагерра (1834 1886), являются каноническими решениями Уравнения Лагерра: являющегося линейным дифференциальным уравнением второго порядка. Это уравнение имеет несингулярное решение… … Википедия
Многочлены Лагерра — В математике, Многочлены Лагерра, названные в честь Эдмона Лагерра (1834 1886), являются каноническими решениями Уравнения Лагерра: являющегося линейным дифференциальным уравнением второго порядка. Многочлены Лагерра также используются в… … Википедия
ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ — системыполиномов , п =0, 1, ..., ортогональных с весом на интервале ( а, b): где квадрат нормы. Подобные системы возникают в разл. задачах матем. физики:в теории представлений групп, в вычислит. математике, при решении задачна собственные… … Физическая энциклопедия
Атом водорода — Атом водорода физическая система, состоящая из атомного ядра, несущего элементарный положительный электрический заряд, и электрона, несущего элементарный отрицательный электрический заряд. В состав атомного ядра может входить протон или… … Википедия
Многочлены Эрмита — Многочлены Эрмита определённого вида последовательность многочленов одной вещественной переменной. Многочлены Эрмита возникают в теории вероятностей, в комбинаторике, физике. Эти многочлены названы в честь Шарля Эрмита. Содержание 1… … Википедия
 , являются последовательностью полиномов, которая может быть найдена по Формуле Родригеса
, являются последовательностью полиномов, которая может быть найдена по Формуле Родригеса
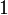
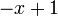
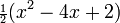
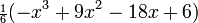
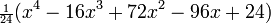
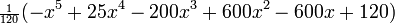
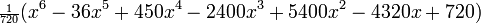
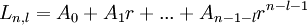
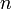 — главное (орбитальное) квантовое число;
— главное (орбитальное) квантовое число;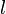 — орбитальное (азимутальное) квантовое число.
— орбитальное (азимутальное) квантовое число.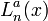 являются решениями уравнения:
являются решениями уравнения: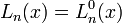 .
.