- СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- СПЕЦИАЛЬНЫЕ ФУНКЦИИ
-
- отдельные классы функций, возникающих вомногих теоретич. и прикладных задачах, обычно при решении дифференц. ур-ний. <В физике чаще всего встречаются гамма-функция (см. Эйлера интегралы),ортогональные полиномы, сферические функции, цилиндрические функции, гипергеометрическиефункции и вырожденные гипергеометрические функции, параболическогоцилиндра функции, интегральные синус и косинус, интеграл вероятности(см. Интегральные функции), Матьё функции, эллиптические функции идр. Все перечисленные ф-ции, за исключением гамма-функции, ф-ций Матьёи эллиптич. ф-ций, являются решениями обыкновенного дифференц. ур-ния 2-гопорядка:
где
- полиномы, степень к-рых не выше 2,
- полином, степень к-рого не выше 1, z - комплексная переменная.Напр., ур-ние Бесселя
является частным случаем ур-ния (1) при
,
,
. Спомощью замены и=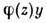
и выбора ф-ции 
ур-ние (1) можно привести к виду:
[
- полином, <степень к-poгo не выше 1,
-постоянная]. При 
ур-ние (2) имеет полиномиальные решения, определяемые ф - л о й Р од р и г а:
[В п - нормировочная постоянная, п - степеньполинома, ф-ция
удовлетворяет ур-нию 
],к-рые после линейной замены переменной переходят в классич. ортогональныеполиномы (полиномы Якоби, Лагерра и Эрмита).Ур-ние (2) в зависимости от степени полинома
можно привести к следующим канонич. видам:
(гипергеометрическое уравнение Гаусса),
(вырожденное гипергеометрическое уравнение),
(уравнение Эрмита).
Обобщая ф-лу Родрига (4), можно получить в явном виде частные решенияур-ния (2) при произвольных
в виде интегрального представления 
где величина v связана с
соотношением, аналогичным соотношению (3):
ф-ция
- решение ур-ния 
контур С - отрезок прямой (s1, s2), наконцах к-рого выполнено условие:
Контуры такого вида можно выбрать лишь при нек-рых ограничениях, наложенныхна коэф. ур-ния (2). Распространение результатов, полученных при такихограничениях, на более общие случаи можно получить с помощью аналитич. <продолжения решений. Из интегрального представления (5) легко вывести всесвойства перечисленных С. ф.: разложения в степенные ряды, разл. функциональныесоотношения, асимптотич. разложения и др.
При помощи аналогичных рассуждений можно построить теорию разностныханалогов С. ф., в частности классич. ортогональных полиномов дискретнойпеременной на равномерных и неравномерных сетках.
С. ф. возникают обычно при разделении переменных и отыскании собств. <ф-ций дифференц. операторов в нек-рых системах координат. Такие операторычасто инвариантны относительно к.-л. группы преобразований, к-рые переводятсобств. ф-ции оператора в собств. ф-ции, отвечающие тому же собств. значению. <Т. о., каждому элементу группы ставится в соответствие линейное преобразованиев пространстве собств. ф-ций, наз. представлением группы. Поэтомусуществует связь между С. ф. и матричными элементами представлений групп. <Используя свойства представлений, можно получить разд. ф-лы для С. ф.,напр. ф-лы сложения, интегральные представления, рекуррентные ф-лы.
Так, представления группы движения евклидовой плоскости связаны с цилиндрич. <ф-циями, представления группы вещественных унимодулярных матриц 2-го порядка- с гипергеом. ф-циями. Особенно часто в физике используют представлениягруппы вращений трёхмерного пространства, с ними связаны Вигнера функции, <Клебша - Гордана коэффициенты, и Вигнера 6j-символы, к-рые можновыразить через ортогональные полиномы непрерывного или дискретного аргумента. <Напр., ф-ции Вигнера удаётся записать с помощью полиномов Якоби или полиномовКравчука. Коэф. Клебша-Гордана и 6j -символы Вигнера можно выразитьчерез полиномы Хана и полиномы Рака.
Лит.: Б е и т м е н Г., Э р д е й и А., Высшие трансцендентныефункции, пер. с англ., 2 изд., т. 1-2, М., 1973-74; Виленкин Н. Я., Специальныефункции и теория представлений групп, 2 изд., М., 1991; Никифоров А. Ф.,Уваров В. Б., Специальные функции математической физики, 2 изд., М., 1984;Справочник по специальным функциям, пер. с англ., М., 1979. А. Ф. Никифоров.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
