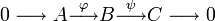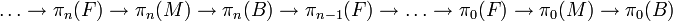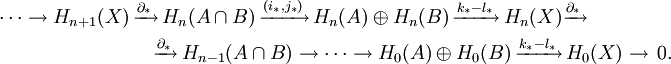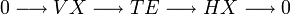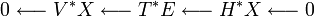Короткая точная последовательность
- Короткая точная последовательность
-
Точная последовательность — последовательность алгебраических объектов Gi с последовательностью гомоморфизмов 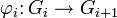 , такая что для любого i образ
, такая что для любого i образ 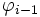 совпадает с ядром
совпадает с ядром 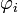 (если оба гомоморфизма с такими индексами существуют).
(если оба гомоморфизма с такими индексами существуют).
В большинстве приложений роль Gi играют коммутативные группы, иногда векторные пространство или алгебры над кольцами.
Связанные определения
- Точные последовательности типа
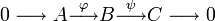
- называются короткими точными последовательностями, в этом случае
 — мономорфизм, а ψ — эпиморфизм.
— мономорфизм, а ψ — эпиморфизм.
- При этом, если у
 есть правый обратный или у ψ левый обратный морфизм, то B можно отождествить с
есть правый обратный или у ψ левый обратный морфизм, то B можно отождествить с 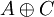 таким образом, что A и C отображаются в A и C тождественным образом. В этом случае короткая точная последовательность называется расщепляющейся.
таким образом, что A и C отображаются в A и C тождественным образом. В этом случае короткая точная последовательность называется расщепляющейся.
- Если
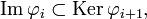 то последовательность называется полуточной.
то последовательность называется полуточной.
Примеры
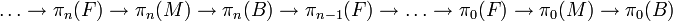
- Точная последовательность Майера — Вьеториса имеет большое значение для вычисления групп гомологий сложных пространств:
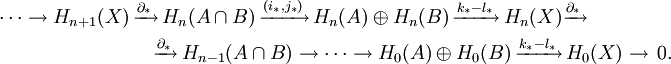
-
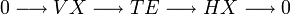
- и двойственная к ней
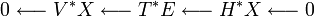
- Здесь TE — касательное расслоение к многообразию E, VX и HX — вертикальное и горизонтальное расслоения к X соответственно. * обозначает двойственное расслоение (кокасательное и т. п.).
Литература
- ↑ Спеньер Э. Алгебраическая топология. — М.: Мир, 1971.
- ↑ Г. А. Сарданашвили Современные методы теории поля. Т.1: Геометрия и классические поля, — М.: УРСС, 1996. — 224 с.
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Короткая точная последовательность" в других словарях:
Точная последовательность — Точная последовательность последовательность алгебраических объектов с последовательностью гомоморфизмов , такая что для любого образ совпадает с ядром (если оба гомоморфизма с такими индексами существуют). В большинстве приложений роль … Википедия
Полуточная последовательность — Точная последовательность последовательность алгебраических объектов Gi с последовательностью гомоморфизмов , такая что для любого i образ совпадает с ядром (если оба гомоморфизма с такими индексами существуют). В большинстве приложений роль Gi… … Википедия
Нуклеотидная последовательность — Распечатка электрофореграммы, полученной с помощью автоматического секвенатора Нуклеотидная последовательность, генетическая последовательность порядок следования нуклеотидных остатков в нуклеиновых кислотах. Определяется при помощи… … Википедия
Теорема об универсальных коэффициентах — в алгебраической топологии устанавливает связь между целочисленными гомологиями топологического пространства X и его гомологиями с коэффициентами в произвольной абелевой группе A. Она утверждает, что группы целочисленных гомологий полностью… … Википедия
ХАРАКТЕРИСТИЧЕСКИЙ КЛАСС — естественное сопоставление с каждым расслоением (как правило, векторным) определенного типа нек рого класса когомологий базы В(наз. X. к. данного расслоения). Естественность означает, что X. к. расслоения, индуцированного отображением совпадает с … Математическая энциклопедия
Спинорная группа — Запрос «Spin» перенаправляется сюда; о музыкальном журнале см. Spin (журнал). Спинорная группа подмножество элементов алгебры Клиффорда над (со скалярным произведением), состоящее из элементов вида , где единичные векторы. Операцией… … Википедия
Теория кос — Пример косы с тремя дугами. Теория кос раздел топологии и алгебры, изучающий косы и группы кос, составленные из их классов эквивалентности … Википедия
Spin(n) — Спинорная группа подмножество элементов алгебры Клиффорда над V (со скалярным произведением), состоящее из элементов вида , где единичные векторы. Операцией в спинорной группе является умножение в алгебре Клиффорда. Спинорная группа над… … Википедия
Группа кос — Пример косы с тремя дугами. Теория кос раздел топологии и алгебры, изучающий косы и группы кос, составленные из их классов эквивалентности. Содержание 1 Определение косы 2 Группа кос … Википедия
ОТНОСИТЕЛЬНАЯ ГОМОЛОГИЧЕСКАЯ АЛГЕБРА — гомологическая алгебра, ассоциированная с парой абелевых категорий и фиксированным функтором . Функтор предполагается аддитивным, точным и полным. Короткая точная после довательность объектов категории наз. допустимой, если точная… … Математическая энциклопедия
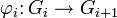 , такая что для любого i образ
, такая что для любого i образ 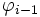 совпадает с ядром
совпадает с ядром 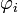 (если оба гомоморфизма с такими индексами существуют).
(если оба гомоморфизма с такими индексами существуют). — мономорфизм, а ψ — эпиморфизм.
— мономорфизм, а ψ — эпиморфизм.
 есть правый обратный или у ψ левый обратный морфизм, то B можно отождествить с
есть правый обратный или у ψ левый обратный морфизм, то B можно отождествить с 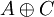 таким образом, что A и C отображаются в A и C тождественным образом. В этом случае короткая точная последовательность называется расщепляющейся.
таким образом, что A и C отображаются в A и C тождественным образом. В этом случае короткая точная последовательность называется расщепляющейся.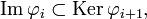 то последовательность называется полуточной.
то последовательность называется полуточной.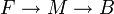 — локально тривиальное расслоение над B со слоем F, то следующая последовательность гомотопических групп точна[1]:
— локально тривиальное расслоение над B со слоем F, то следующая последовательность гомотопических групп точна[1]: — локально тривиальное расслоение многообразий. Тогда с ним связана[2] короткая точная последовательность расслоений
— локально тривиальное расслоение многообразий. Тогда с ним связана[2] короткая точная последовательность расслоений