Группа кос

Пример косы с тремя дугами.

Теория кос — раздел топологии и алгебры, изучающий косы и группы кос, составленные из их классов эквивалентности.

Определение косы

Коса из n нитей — объект, состоящий из двух параллельных плоскостей P₀ и P₁ в трёхмерном пространстве 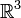$\R^3$, содержащих упорядоченные множества точек $a_1,a_2,\dots,a_n\in P_0$ и $b_1,b_2,\dots,b_n\in P_1$ и из n непересекающихся между собой простых дуг $l_1,l_2,\dots,l_n$, пересекающих каждую параллельную плоскость P_t между P₀ и P₁ однократно и соединяющих точки {a_i} с точками {b_i}.

Обычно считается, что точки $a_1,a_2,\dots,a_n$ лежат на прямой l₀ в P₀, а точки $b_1,b_2,\dots,b_n$ на прямой l₁ в P₁, параллельной l₀, причем a_i расположены под b_i для каждого i.

Косы изображаются в проекции на плоскость, проходящую через l₀ и l₁, эта проекция может быть приведена в общее положение так, что имеется только конечное число двойных точек, попарно лежащих в разных уровнях, и пересечения трансверсальны.

Группа кос

Во множестве всех кос с n нитями и с фиксированными P₀,P₁,{a_i},{b_i} вводится отношение эквивалентности. Оно определяется гомеоморфизмами $h:\Pi\to \Pi$, где Π — область между P₀ и P₁, тождественными на $P_0\cup P_1$. Косы α и β эквивалентны, если существует такой гомеоморфизм h, что h(α) = β.

Классы эквивалентности, далее также называемые косами, образуют группу кос B(n). Единичная коса класс эквивалентности, содержащий косу из n параллельных отрезков. Коса α ^{- 1}, обратная косе α, определяется отражением в плоскости P_{1 / 2}

Нить косы соединяет a_i с $b_{j_i}$ и определяет подстановку, элемент симметрической группы S_n. Если эта подстановка тождественна, то коса называется крашеной (или чистой) косой. Это отображение задаёт эпиморфизм B(n) на группу S_n перестановок n элементов, ядром которого является подгруппа K(n), соответствующая всем чистым косам, так что имеется короткая точная последовательность

$0 \to K(n)\to B(n)\to S _n\to 0$

См. также

• Теория узлов

Литература

• Сосинский А., Косы и узлы. Квант № 2, 1989, стр. 6-14