ХАРАКТЕРИСТИЧЕСКИЙ КЛАСС

ХАРАКТЕРИСТИЧЕСКИЙ КЛАСС

-естественное сопоставление с каждым расслоением 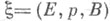(как правило, векторным) определенного типа нек-рого класса когомологий базы В(наз. X. к. данного расслоения). Естественность означает, что X. к. расслоения, индуцированного отображением совпадает с образом при X. к. расслоения над В. Характеристический класс многообразия - класс когомологий многообразия, являющийся X. к. его касательного расслоения. X. к. многообразий связаны с важными топологич. характеристиками многообразий, такими, как ориентируемость, эйлерова характеристика, сигнатура и т. д.

Примеры.
Ориентируемость расслоения. Имеет место точная последовательность групп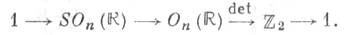


Отображение

сопоставляет с каждым действительным векторным расслоением класс 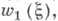к-рый наз. первым классом IIIтифеля - Уитни расслоения 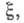здесь 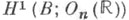- когомологий с коэффициентами в пучке ростков непрерывных функций со значениями в (см. G-Расслоение). Точная когомологич. последовательность показывает, что группа расслоения 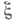редуцируется к т. е. расслоение ориентируемо тогда и только тогда, когда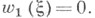
Первый класс Чжэня. Дана короткая точная последовательность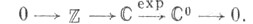

Связывающий гомоморфизм 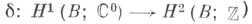соответствующей когомологич. последовательности сопоставляет с каждым одномерным комплексным расслоением над Вдвумерный класс когомологий базы В, наз. первым классом Чжэня расслоения и обозначаемый Иными словами, если 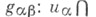-функции перехода расслоения 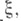то выбором произвольных значений логарифмов 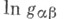получается двумерный целочисленный коцикл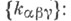

и 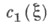есть по определению класс когомологий этого коцикла.
Спинорная структура. Имеет место точная последовательность групп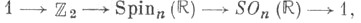


где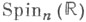 -группа, определяемая в теории Клиффорда алгебр. Связывающее отображение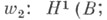 соответствующей когомологич. последовательности наз. вторым классом Штифеля - Уитни. Структурная группа ориентированного векторного расслоения 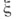может быть редуцирована к тогда и только тогда, когда
Класс Эйлера. Пусть база Вдействительного векторного расслоения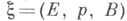 есть гладкое компактное N-мерное многообразие с краем (возможно пустым), и нулевое сечение приведено в лобщее положение с самим собой


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужна курсовая?

Полезное


Смотреть что такое "ХАРАКТЕРИСТИЧЕСКИЙ КЛАСС" в других словарях:

  • характеристический класс продукции — 2.16 характеристический класс продукции (product characterization class): Совокупность продукции, которая выполняет идентичные функции и обладает рядом общих свойств (характеристик). Примечание Характеристические классы с частичным заданием… …   Словарь-справочник терминов нормативно-технической документации

  • нижний характеристический класс — 2.11 нижний характеристический класс (leaf characterization class): Характеристический класс, который не может быть подразделен на какие либо другие классы (подклассы). Источник …   Словарь-справочник терминов нормативно-технической документации

  • Класс Понтрягина — характеристический класс, определенный для вещественных векторных расслоений. Введены в 1947 году советским математиком Л. С. Понтрягиным. Для векторного расслоения с базой классы Понтрягина обозначаются символом и полагаются равными , где ко …   Википедия

  • Класс Штифеля — Уитни — Класс Штифеля  Уитни  определённый характеристический класс, соответствующий вещественному векторному расслоению . Обычно обозначается через w(E). Принимает значения в , кольце когомологий с коэффициентами в . Компонента w(E) в i ых… …   Википедия

  • Класс Штифеля — Класс Штифеля  Уитни  определённый характеристический класс, соответствующий вещественному векторному расслоению . Обычно обозначается через . Принимает значения в , кольце когомологий с коэффициентами в . Компонента в х когомологиях …   Википедия

  • класс — См. разряд …   Словарь синонимов

  • ПОНТРЯГИНА КЛАСС — характеристический класс, определенный для действительных векторных расслоений; П. к. введены в 1947 Л. С. Понтрягиным [1]. Для векторного расслоения x с базой ВП. к. обозначаются символом и полагаются равными , где комилексификация расслоения x …   Математическая энциклопедия

  • ЧЖЭНЯ КЛАСС — характеристический класс, определенный для комплексных векторных расслоений. Ч. к. комплексного векторного расслоения с базой Вобозначается и определен для всех натуральных индексов i. Полным Ч. к. наз. неоднородный характеристич. класс… …   Математическая энциклопедия

  • ШТИФЕЛЯ - УИТНИ КЛАСС — характеристический класс со значениями в определенный для действительных векторных расслоений. Ш. У. к. обозначаются через wi, i>0, и для действительного векторного расслоения над топологич. пространством Вкласс лежит в введены Э. Штифелем [1] и… …   Математическая энциклопедия

  • ТОДДА КЛАСС — характеристический класс комплексного расслоения равный где мультипликативная последовательность, отвечающая степенному ряду Чжэня классы. Введен Дж. Тоддом [1]. Лит.:[1] Тоdd J., лРгос. Lond. Math. Soc …   Математическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»