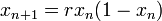- Квадратичное отображение
-
Логистическое отображение (также известное, как квадратичное отображение или отображение Фейгенбаума) является полиномиальным отображением, хрестоматийно упоминаемым в качестве типичного примера того, как сложное, хаотическое поведение может возникать из очень простых нелинейных уравнений. Отображение является дискретным аналогом непрерывного логистического уравнения Ферхюльста, отражая тот факт, что прирост популяции происходит в дискретные моменты времени. Математическая формулировка отображения
где:
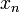 принимает значения от 0 до 1 и отражает численность популяции в
принимает значения от 0 до 1 и отражает численность популяции в 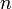 -ом году, а
-ом году, а 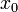 обозначает начальную численность (в год номер 0)
обозначает начальную численность (в год номер 0) - положительный параметр, характеризующий скорость размножения (роста) популяции.
- положительный параметр, характеризующий скорость размножения (роста) популяции.
Это нелинейное отображение описывает два эффекта:
- размножение популяции, со скоростью, пропорциональной ее численности в момент, когда численность мала.
- конкуренцию (смертность при высокой плотности) за жизненные ресурсы, при которой скорость размножения падает из-за ограничения на "максимальную емкость" среды, в которой обитает популяция.
Одним из недостатков использования отображения в качестве демографической модели является тот факт, что при некоторых начальных значениях и величинах параметров отображение дает отрицательные значения численности популяции. Подобного недостатка лишена дискретная модель Рикера, которая также демонстрирует хаотическое поведение.
Зависимость поведения от параметра

При изменении значения параметра
 , в системе наблюдается следующее поведение [1]:
, в системе наблюдается следующее поведение [1]:- если
 больше 0 и меньше 1, популяция в конце концов вымрет, независимо от начальных условий.
больше 0 и меньше 1, популяция в конце концов вымрет, независимо от начальных условий. - если
 больше 1 и меньше 2, численность популяции быстро выйдет на стационарное значение
больше 1 и меньше 2, численность популяции быстро выйдет на стационарное значение
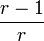 , независимо от начальных условий .
, независимо от начальных условий .
- если
 больше 2 и меньше 3, численность популяции точно так же прийдет к тому же стационарному значению
больше 2 и меньше 3, численность популяции точно так же прийдет к тому же стационарному значению
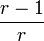 , но вначале будет несколько колебаться вокруг него. Скорость сходимости линейна везде, кроме значения
, но вначале будет несколько колебаться вокруг него. Скорость сходимости линейна везде, кроме значения  =3, при котором она крайне мала, меньше линейной.
=3, при котором она крайне мала, меньше линейной.
- если
 больше 3 и меньше
больше 3 и меньше 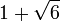 (приблизительно 3.45), численность популяции будет бесконечно колебаться между двумя значениями, причем их величина не зависит от
(приблизительно 3.45), численность популяции будет бесконечно колебаться между двумя значениями, причем их величина не зависит от  .
. - если
 больше 3.45 и меньше 3.54 (приблизительно), то численность популяции будет бесконечно колебаться между четырьмя значениями.
больше 3.45 и меньше 3.54 (приблизительно), то численность популяции будет бесконечно колебаться между четырьмя значениями. - при значении
 больше 3.54, численность популяции будет колебаться между 8 значениями, потом 16, 32 и так далее. Длина интервала изменения параметра, при котором наблюдаются колебания между одинаковым количеством значений, уменьшается по мере увеличения
больше 3.54, численность популяции будет колебаться между 8 значениями, потом 16, 32 и так далее. Длина интервала изменения параметра, при котором наблюдаются колебания между одинаковым количеством значений, уменьшается по мере увеличения  . Отношение между двумя длинами смежных интервалов стремится к константе Фейгенбаума, равной δ = 4.669
. Отношение между двумя длинами смежных интервалов стремится к константе Фейгенбаума, равной δ = 4.669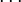 . Подобное поведение является типичным примером каскада бифуркаций удвоения периода.
. Подобное поведение является типичным примером каскада бифуркаций удвоения периода. - При значении
 приблизительно равном 3.57, начинается хаотическое поведение, а каскад удвоений заканчивается. Колебания больше не наблюдаются. Небольшие изменения в начальных условиях приводят к несопоставимым отличиям дальнейшего поведения системы во времени, что является основной характеристикой хаотического поведения.
приблизительно равном 3.57, начинается хаотическое поведение, а каскад удвоений заканчивается. Колебания больше не наблюдаются. Небольшие изменения в начальных условиях приводят к несопоставимым отличиям дальнейшего поведения системы во времени, что является основной характеристикой хаотического поведения. - Большинство значений, превышающих 3.57 демонстрируют хаотическое поведение, однако существуют узкие, изолированные "окна" значений
 , при которых система ведет себя регулярно, обычно их называют "окнами периодичности". К примеру, начиная со значения
, при которых система ведет себя регулярно, обычно их называют "окнами периодичности". К примеру, начиная со значения 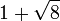 (приблизительно 3.83), существует интервал параметров
(приблизительно 3.83), существует интервал параметров  , при котором наблюдаются колебания между тремя значениями, а для больших значений
, при котором наблюдаются колебания между тремя значениями, а для больших значений  - между 6, потом 12 и т.д. Фактически, в системе можно найти периодические колебания с любым количеством значений. Последовательность смены количества значений удовлетворяет порядку Шарковского.
- между 6, потом 12 и т.д. Фактически, в системе можно найти периодические колебания с любым количеством значений. Последовательность смены количества значений удовлетворяет порядку Шарковского. - При
 = 4, значения отображения покидают интервал [0,1] и расходятся при любых начальных условиях.
= 4, значения отображения покидают интервал [0,1] и расходятся при любых начальных условиях.
Итог вышеперечисленного приведен на бифуркационной диаграмме. По оси абсцисс отложены значения параметра
 , а по оси ординат - принимаемые на больших временах значения
, а по оси ординат - принимаемые на больших временах значения 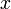 .
. Бифуркационная диаграмма логистического отображения
Бифуркационная диаграмма логистического отображенияСтруктура бифуркационной диаграммы фрактальна: если увеличить область, к примеру, при значении
 = 3.82 в одном из трех ответвлений, то можно увидеть, что тонкая структура этой области выглядит, как искаженная и размытая версия всей диаграммы. То же самое верно для любой окрестности нехаотических точек. Это пример глубокой связи между хаотическими системами и фракталами.
= 3.82 в одном из трех ответвлений, то можно увидеть, что тонкая структура этой области выглядит, как искаженная и размытая версия всей диаграммы. То же самое верно для любой окрестности нехаотических точек. Это пример глубокой связи между хаотическими системами и фракталами.Аналитическое решение
Для
 = 2 точное аналитическое решение выглядит следующим образом:
= 2 точное аналитическое решение выглядит следующим образом: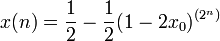
Ссылки
- ↑ "Java-демонстрация бифуркаций квадратичного отображения" at homepage of Dr Evgeny Demidov.
Wikimedia Foundation. 2010.