- ЛИНЕЙНАЯ СИСТЕМА
- семейство эффективных линейно эквивалентных дивизоров на алгебраич. многообразии, параметризованное проективным пространством.
Пусть X - неособое алгебраич. многообразие над полем k,
- обратимый пучок на X, Г (X, 
) - пространство глобальных сечений пучка 
а 
- некоторое конечномерное подпространство. Если dimL>0, то дивизоры, определяемые нулями сечений из L, линейно эквивалентны и эффективны. Линейной системой наз. проективное пространство 
одномерных подпространств в L, параметризующее эти дивизоры. Если 
то Л. с. 
наз. полной; она обозначается также |L|.
Пусть s0, . . ., sn - базис в L. Он определяет рациональное отображение
по формуле
Обычно говорят, что
задано Л. с. |L|. Образ 
не лежит ни в какой гиперплоскости в Р п (см. [2]).
Обратно, каждое рациональное отображение
обладающее этим свойством, задается нек-рой Л. с.
Неподвижной компонентой Л. с. |L| наз. такой эффективный дивизор D* на X, что D=D+D* для любого
где D' - эффективный дивизор. Когда Dпробегает Л. с. |L|, дивизоры D' образуют нек-рую Л. с. |L'| той же размерности, что и Л. с. |L|. Отображение 
совпадает с 
Поэтому при рассмотрении отображения 
можно предполагать, что Л. с. |L| не имеет неподвижных компонент. В этом случае jL не определено в точности на базисном множестве Л. с. |L|.
Примеры. 1) Пусть Х=Р 2 и
тогда сечения 
) отождествляются с формами степени dна Р 2, а полная Л. с.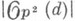 
- с множеством всех кривых степени d.
2) Стандартное квадратичное преобразование т:
(см. Кремоново преобразование).задается Л. с. коник, проходящих через точки (О, О, 1), (О, 1, 0), (1, 0, 0).
3) Инволюция Гейзера
задается Л. с. кривых степени 8, проходящих с кратностью 3 через
7 точек в общем положении.
4) Инволюция Бертини
задается Л. с. кривых степени 17, проходящих с кратностью 6 через 8 точек в общем положении.
Лит.:[1] Алгебраические поверхности, М., 1965 (Тр. Матем. ин-та АН СССР, т. 75); [2] М а м ф о р д Д., Лекции о кривых на алгебраической поверхности, пер. с англ., М., 1968; [3] Zariski О., Algebraic surfaces, 2 ed., В.- Hdlb. - N. Y., 1971. В. А. Псковских.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
