Канторовское множество

Ка́нторово мно́жество есть один из простейших фракталов, подмножество единичного отрезка вещественной прямой, которое является классическим примером «плохого множества» в математическом анализе. Описано в 1883 году Г. Кантором.

Определения

Классическое построение

Из единичного отрезка C₀ = [0,1] удалим среднюю треть, т. е. интервал (1 / 3,2 / 3) Оставшееся точечное множество обозначим через C₁. Множество $C_1=[0,1/3]\cup[2/3,1]$ состоит из двух отрезков; удалим теперь из каждого отрезка его среднюю треть, и оставшееся множество обозначим через C₂. Повторив эту процедуру опять, удаляя средние трети у всех четырёх отрезков, получаем C₃. Дальше таким же образом получаем $C_4,\ C_5,\ C_6,\cdots$. 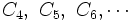Обозначим через C пересечение всех C_i. Множество C называется Канторовым множеством.

Множества 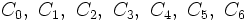$C_0,\ C_1,\ C_2,\ C_3,\ C_4,\ C_5,\ C_6$

С помощью троичной записи

Канторово множество может быть также определено как множество чисел от нуля до единицы, которые можно представить в троичной записи с помощью только нулей и двоек. При этом следует отметить, что число принадлежит Канторовому множеству, если у него есть одно такое представление, например 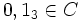$0,1_3\in C$ так как 0,1₃ = 0,0(2)₃.

Как аттрактор

Рассмотрим все последовательности точек {x_n} такие, что для любого n,

x_{n + 1} = x_n / 3 или x_{n + 1} − 1 = (x_n − 1) / 3.

Тогда множество пределов всех таких последовательностей является Канторовым множеством.

Свойства

• Канторово множество замкнуто.
• Канторово множество континуально. В частности,
  • Канторово множество не счётно
• Канторово множество имеет топологическую размерность 0.
• Канторово множество имеет промежуточную (т.е. не целую) Хаусдорфову размерность равную 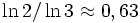$\ln2/\ln3\approx 0,63$. В частности,
  • Канторово множество имеет нулевую меру Лебега.

См. также

• Канторова лестница