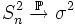- Исправленная выборочная дисперсия
-
Выборочная дисперсия в математической статистике - это оценка теоретической дисперсии распределения на основе выборки. Различают выборочную дисперсию и несмещённую или исправленную выборочные дисперсии.
Содержание
Определения
Пусть
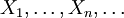 - выборка из распределения вероятности. Тогда
- выборка из распределения вероятности. Тогда- Выборочная дисперсия - это случайная величина
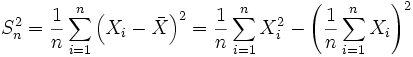 ,
,
где символ
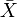 обозначает выборочное среднее.
обозначает выборочное среднее.- Несмещённая (исправленная) дисперсия - это случайная величина
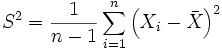 .
.
Замечание
Очевидно,
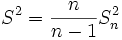 .
.
Свойства выборочных дисперсий
- Выборочная дисперсия является теоретической дисперсией выборочного распределения. Более точно, пусть
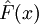 - выборочная функция распределения данной выборки. Тогда для любого фиксированного
- выборочная функция распределения данной выборки. Тогда для любого фиксированного 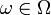 функция
функция 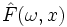 является (неслучайной) функцией дискретного распределения. Дисперсия этого распределения равна
является (неслучайной) функцией дискретного распределения. Дисперсия этого распределения равна 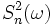 .
.
- Обе выборочные дисперсии являются состоятельными оценками теоретической дисперсии. Если
![\mathrm{D}[X_i] = \sigma^2 < \infty](/pictures/wiki/files/100/d6d796e81d9e3a8ecb0060e7ca4b344f.png) , то
, то
и
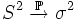 ,
,
где
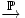 обозначает сходимость по вероятности.
обозначает сходимость по вероятности.- Выборочная дисперсия является смещённой оценкой теоретической дисперсии, а исправленная выборочная дисперсия несмещённая:
![\mathbb{E}\left[S^2_n\right] = \frac{n-1}{n}\sigma^2](/pictures/wiki/files/101/e6ea5f344d7f3045c73a0b7b3f0105ae.png) ,
,
и
![\mathbb{E}\left[S^2\right] = \sigma^2](/pictures/wiki/files/102/fd42b1e59aff2b3990b64ace98334974.png) .
.
- Выборочная дисперсия нормального распределения имеет распределение хи-квадрат. Пусть
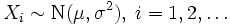 . Тогда
. Тогда
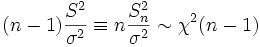 .
.
Оценки СКО
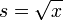
Смотрите также
Wikimedia Foundation. 2010.