- Интерполяционный ряд
-
Интерполяцио́нные ряды́ вошли в математику в основном благодаря Ньютону. Первые их примеры - бесконечный интерполяционный ряд Ньютона и ряд Тейлора. В XVIII в. бесконечными интерполяционными рядами как инструментом математического анализа широко пользовались Эйлер, Лагранж и Лаплас, в XIX в. – Гаусс, Абель и Коши. В конце XIX в. обобщение задач интерполирования послужило одним из источников проблемы моментов в работах Чебышёва, Стилтьеса и Маркова.
Построение интерполяционного ряда, или интерполяционный процесс, определяется последовательностью линейных непрерывных функционалов
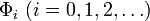 в линейном топологическом пространстве. При этом имеется также такая последовательность функций
в линейном топологическом пространстве. При этом имеется также такая последовательность функций 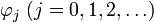 , что
, чтогде
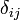 - символ Кронекера (
- символ Кронекера (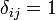 , если
, если 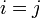 ; иначе
; иначе 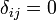 ). Последовательность
). Последовательность 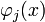 называется базисом фундаментальных полиномов интерполяционного процесса. Интерполяционным рядом функции
называется базисом фундаментальных полиномов интерполяционного процесса. Интерполяционным рядом функции 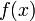 называется формальное выражение
называется формальное выражениеЕсли этот ряд сходится, то его сумма
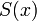 удовлетворяет равенствам
удовлетворяет равенствампри
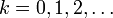 независимо от того, равна сумма
независимо от того, равна сумма 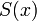 исходной функции
исходной функции 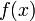 или нет. Совокупность этих равенств выражает обобщение обычной задачи интерполирования функции по ее значениям в последовательности точек.
или нет. Совокупность этих равенств выражает обобщение обычной задачи интерполирования функции по ее значениям в последовательности точек.Литература
- Евграфов М.А. Интерполяционная задача Абеля-Гончарова. М.: Гостехиздат, 1954.
- Ахиезер Н.И. Классическая проблема моментов. М.: Физматлит, 1961.
- Ибрагимов И.И. Методы интерполяции функций и некоторые их применения. М.: Наука, 1971.
- Крейн М.Г., Нудельман А.А. Проблема моментов Маркова и экстремальные задачи. М.: Наука, 1973.
- Головинский И.А. Из истории интерполяционных рядов. // Историко-математические исследования. М.: Наука, вып. XXII, 1977, с. 65-81.
- Головинский И.А. Интерполяционные ряды Лапласа. // Историко-математические исследования. М.: Наука, вып. XXIV, 1979, с. 104-120.
Wikimedia Foundation. 2010.

![\Phi_i[\varphi_j] = \delta_{ij},](/pictures/wiki/files/99/cc70bfa71e295de0715347e5a96b50b7.png)
![\sum_{i=k}^\infty\Phi_k[f]\varphi_k(x) .](/pictures/wiki/files/49/14d760ba56c0e2277c902c7162c78888.png)
![\textstyle \Phi_k[S(x)] = \Phi_k[f(x)]](/pictures/wiki/files/49/1a5274ad666735c6dd60a3b5dc396ecd.png)