ИНТЕРПОЛИРОВАНИЕ ОПЕРАТОРОВ

- получение из известных свойств оператора в двух или нескольких пространствах выводов о свойствах этого оператора в нек-рых в определенном смысле промежуточных пространствах. Банаховой парой A, В наз. два банаховых пространства, алгебраически и непрерывно вложенные в отделимое линейное топологич. пространство На пересечении AЗ B вводится норма

на арифметич. сумме А+В- норма

Пространства и А+В банаховы. Банахово пространство Еназ. промежуточным для пары А, В, если

Линейное отображение Т, действующее из A+B в C+D, наз. ограниченным оператором из пары А, В в пару С, D, если его сужение на А(соответственно В)является ограниченным оператором из А(соответственно В) в С (соответственно D). Тройка пространств {А, В, Е} наз. интерполяционнойотносительно тройки {С, D, F},. пространство Е(соответственно F)- промежуточное для пары А, В (соответственно С, D), если всякий ограниченный оператор из пары А, В в пару С, D отображает Ев F. Если А = С, B=D и E=F, то пространство Еназ. интерполяционным между Аи В. Для интерполяционных троек существует константа с такая, что

Первая интерполяционная теорема получена М. Риссом (М. Riesz, 1926): тройка пространств {L_p0 , L_p1, L_p )является интерполяционной относительно тройки {L_q0,L_q1, L_q}, если р ₁ , q₀, и при нек-ром qО(0, 1)

Мера, по к-рой строятся перечисленные пространства, может быть своей для каждой тройки. Аналог этой теоремы может не быть справедливым для других классич. семейств пространств; напр., пространство С ¹(0, 1) не является интерполяционным между С (0, 1) и С ²(0, 1).

Интерполяционным функтором Fназ. функтор, ставящий в соответствие каждой банаховой паре А, В промежуточное пространство F(A, В), причем для любых двух банаховых пар А, В и С, D тройки {А, B, F(A, В)}и {С, D, F(C, D ))являются друг относительно друга интерполяционными. Имеется ряд методов построения интерполяционных функторов. Наибольшее число приложений нашли два из них.

К-м етод Петре. Для банаховой пары А, Встроится функционал

эквивалентный при каждом tнорме в A+В. Банахово пространство Gизмеримых на полуоси функций наз. идеальным пространством, если из того, что почти всюду на и вытекает и . Рассматриваются все элементы хиз А+В, для к-рых Они образуют банахово пространство относительно нормы Пространство будет ненулевым и промежуточным для А, Вв том и только в том случае, когда функция min {t, 1} принадлежит G. В этом случае функтор будет интерполяционным. Для нек-рых банаховых пар функционал K(t, х )вычисляется, и это позволяет эффективно строить интерполяционные пространства. Для пары L₁ и 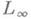где х* (т)- равноизмеримая с функцией хневозрастающая непрерывная справа функция на Для пары С и С ¹ где со (t, x)- модуль непрерывности функции х, а знак означает переход к наименьшей выпуклой мажоранте функции на Для пары ( Соболева пространство)

где

За пространство Gчасто принимается пространство с нормой

Соответствующий функтор обозначается _р.

Важную роль в теории уравнений с частными производными играют пространства Бесова где m=ql. Ряд классич.неравенств анализа уточняется в терминах пространств Лоренца

Комплексный метод Кальдерона- Лионса. Для банаховой пары А, Вчерез Ф (А, В)обозначается пространство, состоящее из всех функций cp(z), определенных в полосе П :комплексной плоскости, со значениями в пространстве А+В, обладающих свойствами: 1) j(z) непрерывна и ограничена по норме А+В в П, 2) j(z) аналитична относительно нормы в А+В внутри П, 3) j(it) непрерывна и ограничена по норме А,4) j(1 + it) непрерывна и ограничена по норме В. Пространство [ А, В]_a, определяется как совокупность всех элементов представимых в виде х=j(a) при В нем вводится норма

Таким образом строится интерполяционный функтор [ А, В]_a. Если А = L _р0 и B = L_p1,то [L_p0, L_P1]_a =L_p, где 1/р=(1- a)/p₀+a/p₁. Если G₀ и G₁- два идеальных пространства, и хотя бы в одном из них норма абсолютно непрерывна, то пространство [G₀, G₁]_a состоит из всех функций x(t), для к-рых |x(t)|=|x₀(t)|^1-a|x₁(t)|^a при нек-рых Если для двух комплексных гильбертовых пространств Н ₀ и Н ₁ имеется вложение то пространства образуют важное для приложений семейство пространств, наз. гильбертовой шкалой. Если H₀=L₂ и H₁= то[H₀, H₁] _а= (пространство Соболева с дробными индексами). О других методах построения интерполяционных функторов, а также об их связях с теорией шкал банаховых пространств см. [1], [3], [5], [8].

Особую роль в теории И. о. играет направление, связанное с интерполяционной теоремой Марцинкевича об операторах слабого типа: оператор Т, действующий из банахова пространства Ав пространство всех измеримых функций, напр., на полуоси, наз. оператором слабого типа ( А, y), если При этом предполагается, что функции y(t) и t/y(t) не убывают (напр., y(t)=t^a, ). Теоремы типа теоремы Марцинкевича позволяют для операторов Тслабых типов (A₀, y₀). и (A₀, y₁) одновременно (A₀, A₁ - банахова пара) описывать пары пространств А, Е, для к-рых Во многих случаях достаточно проверить, что из Ав Едействует оператор

где K(t, x)- функционал Петре для пространств A₀, А ₁. Если действие из Ав Епоказано для всех линейных операторов слабых типов (A_i, y_i), то оно будет иметь место и для квазиаддитивных операторов (со свойством |T(x+y)(t)|b(|Tx(t)|+|Ty(t)|). слабых типов ( А _i, y_i), i =0,1. Многие важные операторы анализа (напр., сингулярный оператор Гильберта) имеют слабый тип в естественных пространствах и поэтому соответствующие интерполяционные теоремы получили многочисленные применения.

Лит.:[1] Butzer P., Berens H., Semi-groups of Operators and Approximation, В., 1967; [2] Зигмунд А., Тригонометрические ряды, пер. с англ., М., 1965; [3] Крейн С. Г., Петунии Ю. И., "Успехи матем. наук", 1966, т. 21, в. 2, с. 89-168; [4] Лионе Ж.-Л., Мадженес Э., Неоднородные граничные задачи и их приложения, пер. с франц., М., 1971; [5] Мадженес Э., "Успехи матем. наук", 1966, т. 21, в. 2, с. 169-218; [6] Стейн И., Вейс Г., Введение в гармонический анализ на евклидовых пространствах, пер. с англ., М., 1974; [7] Функциональный анализ, [Справочная математическая библиотека], 2 изд., М., 1972; [8] Bergh Т. Lofstrom, Interpolation spaces, В., 1976.

С. Г. Крейн.