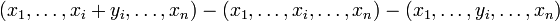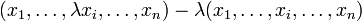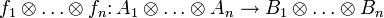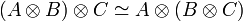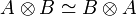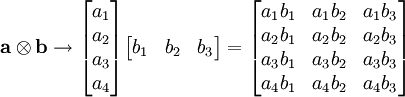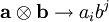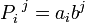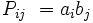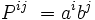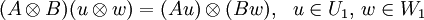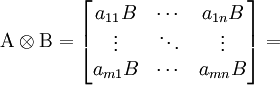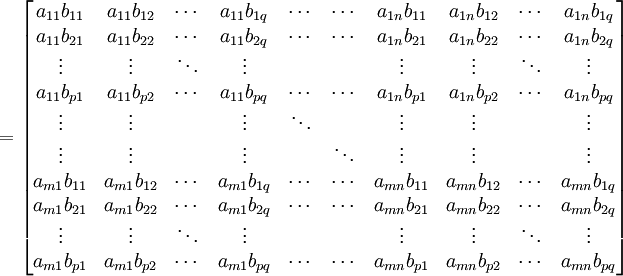Индефинитное произведение

Те́нзорное произведе́ние — одно из основных понятий линейной алгебры.

Тензорное произведение модулей

Пусть 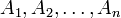$A_1,A_2,\dots,A_n$ — модули над некоторым коммутативным кольцом R. Тензорным произведением модулей называется модуль B над R, данный вместе с полилинейным отображением 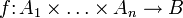$f\colon A_1\times \dots \times A_n \to B$ и обладающий свойством универсальности, то есть такой, что для всякого модуля C над R и любого полилинейного отображения 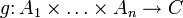$g\colon A_1\times \dots \times A_n \to C$ существует единственный гомоморфизм модулей 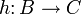$h\colon B \to C$ такой, что диаграмма

коммутативна. Тензорное произведение обозначается 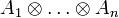$A_1 \otimes\ldots\otimes A_n$. Из универсальности тензорного произведения следует, что оно определено однозначно с точностью до изоморфизма.

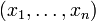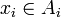Для доказательства существования тензорного произведения любых модулей над коммутативным кольцом построим свободный модуль M, образующими которого будут n-ки элементов модулей $(x_1,\dots,x_n)$ где $x_i \in A_i$. Пусть N — подмодуль M, порождаемый следующими элементами:

1. $(x_1,\dots,x_i + y_i,\dots,x_n) - (x_1,\dots,x_i,\dots,x_n) - (x_1,\dots,y_i,\dots,x_n)$
2. $(x_1,\dots,\lambda x_i,\dots,x_n) - \lambda(x_1,\dots,x_i,\dots,x_n)$

Тензорное произведение определяется как фактор-модуль B = M / N, класс 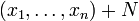$(x_1,\dots,x_n) + N$ обозначается 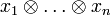$x_1 \otimes \dots \otimes x_n$, и называется тензорным произведением элементов x_i, a f определяется как соответствующее индуцированное отображение.

Из 1) и 2) следует что отображение 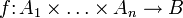$f\colon A_1\times \dots \times A_n \to B$ полилинейно. Докажем, что для для любого модуля C и любого полилинейного отображения 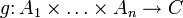$g\colon A_1\times \dots \times A_n \to C$ существует единственный гомоморфизм модулей h, такой, что $g = h \circ f$.

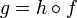В самом деле, так как M свободен, то существует единственное отображение h ^* , делающее диаграмму

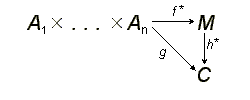
коммутативной, а в силу того, что g полилинейно, то на N h ^* (N) = 0, отсюда, переходя к индуцированному отображению, получаем, что 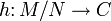$h\colon M/N \to C$, будет тем самым единственным гомоморфизмом, существование которого и требовалось доказать.

Элементы 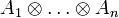$A_1 \otimes \dots \otimes A_n$, представимые в виде 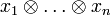$x_1 \otimes \dots \otimes x_n$, называются разложимыми.

Если 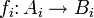$f_i\colon A_i \to B_i$ — изоморфизмы модулей, то индуцированный гомоморфизм, соответствующий билинейному отображению

$f_1\otimes\dots\otimes f_n\colon A_1\otimes\dots\otimes A_n \to B_1\otimes\dots\otimes B_n$

существующий по свойству универсальности, называется тензорным произведением гомоморфизмов f_i.

Особенно простой случай получается в случае свободных модулей. Пусть 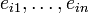$e_{i 1},\dots,e_{i n}$ — базис модуля A_i. Построим свободный модуль F над нашим кольцом, имеющий в качестве базиса элементы, соответствующие n-кам 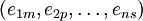$(e_{1 m}, e_{2 p}, \dots, e_{n s})$, определив отображение 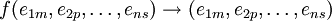$f(e_{1 m}, e_{2 p}, \dots, e_{n s}) \to (e_{1 m}, e_{2 p}, \dots, e_{n s})$ и распространив его на 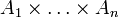$A_1 \times \dots \times A_n$ по линейности. Тогда F является тензорным произведением, где 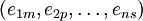$(e_{1 m}, e_{2 p}, \dots, e_{n s})$ является тензорным произведением элементов 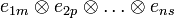$e_{1m} \otimes e_{2p} \otimes \dots\otimes e_{ns}$. Если число модулей и все их базисы конечны, то

$rank (A_1 \otimes \dots \otimes A_n) = rank A_1 \cdot \dots \cdot rank A_n$.

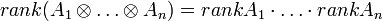Свойства

Из универсальности тензорного произведение легко выводятся следующие его свойства:

• Ассоциативность

$(A \otimes B)\otimes C \simeq A \otimes(B \otimes C)$

• Коммутативность

$A \otimes B \simeq B \otimes A$

• Линейность

$A \otimes (B \oplus C) \simeq (A\otimes B) \oplus (A \otimes C)$

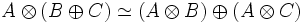
$\oplus$ — внешняя сумма модулей.

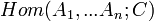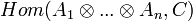• Модули полилинейных отображений $\ Hom(A_1,...A_n; C)$ и $Hom(A_1\otimes ...\otimes A_n, C)$ изоморфны.
• Если A — конечно порожденный проективный модуль, а A^* — его сопряженный, то $A^* \otimes B \simeq Hom(A,B)$

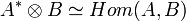
Все эти изоморфизмы естественны.

Тензорное произведение векторных пространств

Так как векторное пространство является свободным модулем, то к ним относится всё предыдущее, для прикладной математики важны следующие частные случаи:

Тензорное произведение двух векторов

(Матричное) умножение вектора-столбца справа на вектор-строку даёт их тензорное произведение:

$\mathbf{a} \otimes \mathbf{b} \rightarrow \begin{bmatrix}a_1 \\ a_2 \\ a_3 \\ a_4\end{bmatrix} \begin{bmatrix}b_1 & b_2 & b_3\end{bmatrix} = \begin{bmatrix}a_1b_1 & a_1b_2 & a_1b_3 \\ a_2b_1 & a_2b_2 & a_2b_3 \\ a_3b_1 & a_3b_2 & a_3b_3 \\ a_4b_1 & a_4b_2 & a_4b_3\end{bmatrix}$

или, если пользоваться верхними и нижними индексами (по повторяющимся индексам подразумевается суммирование):

$\mathbf{a} \otimes \mathbf{b} \rightarrow a_ib^j$

Если же не привязываться к матричной форме записи и матричным операциям, то, как и для тензоров более высокого ранга, прямое произведение будет представлять тензор более высокого ранга (для произведения векторов — второго, то есть с двумя значками) с компонентами, равными произведениям компонент множителей с соответствующими индексами:

$P_i^{\ j} = a_ib^j$

$P_{ij}\ = a_ib_j$

$P^{ij}\ = a^ib^j$

Произведение двух векторов называется также диадным, а результат (тензор второго ранга) — диадой.

Тензорным произведением пространства векторов-столбцов на пространство векторов-строк является пространство матриц.

Тензорное произведение операторов

Пусть 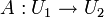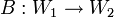$A: U_1 \to U_2$, $B: W_1 \to W_2$ — линейные операторы. Тензорное произведение операторов 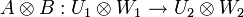$A\otimes B: U_1\otimes W_1 \to U_2\otimes W_2$ определятся по правилу

$(A\otimes B)(u\otimes w) = (A u)\otimes (B w),~~ u\in U_1,\,w\in W_1$

Если матрицы операторов при некотором выборе базисов имеют вид

$\mathrm{A} = \begin{bmatrix} a_{11} & \cdots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{m1} & \cdots & a_{mn} \end{bmatrix}$

$\mathrm{B} = \begin{bmatrix} b_{11} & \cdots & b_{1q} \\ \vdots & \ddots & \vdots \\ b_{p1} & \cdots & b_{pq} \end{bmatrix}$

то матрица их тензорного произведения запишется в базисе, образованном тензорным произведением базисов, в виде блочной матрицы

$\mathrm{A} \otimes \mathrm{B} = \begin{bmatrix} a_{11} B & \cdots & a_{1n}B \\ \vdots & \ddots & \vdots \\ a_{m1} B & \cdots & a_{mn} B \end{bmatrix} =$

$= \begin{bmatrix} a_{11} b_{11} & a_{11} b_{12} & \cdots & a_{11} b_{1q} & \cdots & \cdots & a_{1n} b_{11} & a_{1n} b_{12} & \cdots & a_{1n} b_{1q} \\ a_{11} b_{21} & a_{11} b_{22} & \cdots & a_{11} b_{2q} & \cdots & \cdots & a_{1n} b_{21} & a_{1n} b_{22} & \cdots & a_{1n} b_{2q} \\ \vdots & \vdots & \ddots & \vdots & & & \vdots & \vdots & \ddots & \vdots \\ a_{11} b_{p1} & a_{11} b_{p2} & \cdots & a_{11} b_{pq} & \cdots & \cdots & a_{1n} b_{p1} & a_{1n} b_{p2} & \cdots & a_{1n} b_{pq} \\ \vdots & \vdots & & \vdots & \ddots & & \vdots & \vdots & & \vdots \\ \vdots & \vdots & & \vdots & & \ddots & \vdots & \vdots & & \vdots \\ a_{m1} b_{11} & a_{m1} b_{12} & \cdots & a_{m1} b_{1q} & \cdots & \cdots & a_{mn} b_{11} & a_{mn} b_{12} & \cdots & a_{mn} b_{1q} \\ a_{m1} b_{21} & a_{m1} b_{22} & \cdots & a_{m1} b_{2q} & \cdots & \cdots & a_{mn} b_{21} & a_{mn} b_{22} & \cdots & a_{mn} b_{2q} \\ \vdots & \vdots & \ddots & \vdots & & & \vdots & \vdots & \ddots & \vdots \\ a_{m1} b_{p1} & a_{m1} b_{p2} & \cdots & a_{m1} b_{pq} & \cdots & \cdots & a_{mn} b_{p1} & a_{mn} b_{p2} & \cdots & a_{mn} b_{pq} \end{bmatrix}$

Соответствующая операция над матрицами называется кронекеровским произведением, по имени Л. Кронекера

Литература

• Винберг Э.Б. Курс алгебры. — 3-е изд.. — Москва: Факториал Пресс, 2002. — 544 с. — 3000 экз. — ISBN 5-88688-060-7
• Ленг С. Алгебра. — Москва: Мир, 1967.

См. также

• Тензор
• Внешнее произведение
• Функтор Tor