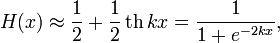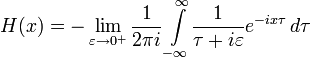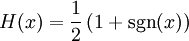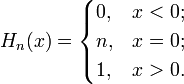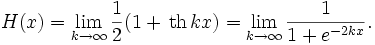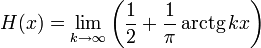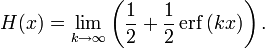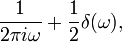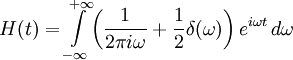- Единичная Хевисайда
-
Функция Хевисайда, единичная ступенчатая функция, ступенька положения — специальная математическая функция, чьё значение равно нулю для отрицательных аргументов и единице для положительных аргументов:
Чаще всего неважно, какое значение функция принимает в нуле (H(0)).
Функция широко используется в математическом аппарате теории управления и обработке сигналов для представления сигналов, включающихся в определённый момент и остающихся включёнными постоянно. Названа в честь Оливера Хевисайда.
Функция Хевисайда является первообразной функцией для дельта-функции Дирака, H' = δ, это также можно записать как:
хотя это выражение не является математически точным.
Содержание
Дискретная форма
Можно определить дискретную функцию Хевисайда как функцию от дискретного аргумента n:
где n — целое число.
Дискретный единичный импульс является первой разностью дискретной функции Хевисайда:
- δ[n] = H[n] − H[n − 1].
Аналитические формы
Для более удобного использования функцию Хевисайда можно аппроксимировать с помощью непрерывной функции:
где большему k соответствует более крутой подъём функции в точке x = 0. Если принять H(0) = 1 / 2, уравнение можно записать в предельной форме:
Запись
Часто используется и бывает полезной интегральная форма записи единичной функции:
H(0)
Значение функции в нуле может быть задано как H(0) = 0, H(0) = 1 / 2 или H(0) = 1. H(0) = 1 / 2 — наиболее часто встречающийся случай, ввиду возрастания симметрии функции и связи её с функцией знака:
Значение в нуле может явно указываться в записи функции:
Существует несколько других аппроксимаций непрерывными функциями:
Преобразование Фурье
Доказано, что производная функции Хевисайда равна дельта-функции. То есть функция Хевисайда — первообразная дельта-функции:
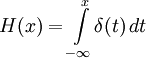 .
.
Следовательно, применив преобразование Фурье к первообразной дельта-функции
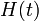 , получим её изображение вида:
, получим её изображение вида:то есть:
(второй член — соответствующий нулевой частоте в разложении — описывает постоянное смещение функции Хевисайда вверх; без него получилась бы нечетная функция).
См. также
Wikimedia Foundation. 2010.


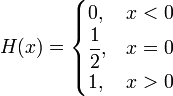
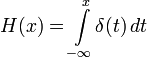
![H[n]=\begin{cases} 0, & n < 0; \\ 1, & n \geqslant 0, \end{cases}](/pictures/wiki/files/57/934fd37f1a30c255b263a7650eae9c75.png)