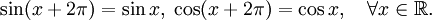- Двоякопериодическая функция
-
 Графики синуса и косинуса — периодических функций с периодом T = 2π.
Графики синуса и косинуса — периодических функций с периодом T = 2π.Периоди́ческая фу́нкция ― функция, повторяющая свои значения через какой-то ненулевой период, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа (периода).
Содержание
Определение
Пусть M есть абелева группа (обычно предполагается
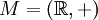 — вещественные числа с операцией сложения или
— вещественные числа с операцией сложения или 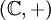 — комплексные числа). Функция
— комплексные числа). Функция 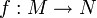 называется периодической с пери́одом
называется периодической с пери́одом 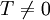 , если справедливо
, если справедливо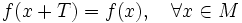 .
.
Если это равенство не выполнено ни для какого
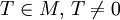 , то функция f называется апериоди́ческой.
, то функция f называется апериоди́ческой.Если для функции
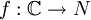 существуют два периода
существуют два периода 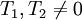 , отношение которых не равно вещественному числу, то есть
, отношение которых не равно вещественному числу, то есть 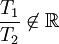 , то f называется двоякопериоди́ческой фу́нкцией. В этом случае значения f на всей плоскости определяются значениями в параллелограме, натянутом на T1,T2.
, то f называется двоякопериоди́ческой фу́нкцией. В этом случае значения f на всей плоскости определяются значениями в параллелограме, натянутом на T1,T2.Замечание
Период функции определён неоднозначно. В частности, если T — период, то и любой элемент T' вида
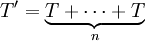 , где
, где 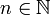 — произвольное натуральное число, также является периодом.
— произвольное натуральное число, также является периодом.Однако если у множества периодов
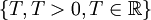 имеется наименьшее значение, то оно называется основным (или главным) периодом функции.
имеется наименьшее значение, то оно называется основным (или главным) периодом функции.Действия с периодическими функциями
Являются неверными утверждения относительно суммы периодических функций:
- Сумма 2 функций с соизмеримыми (даже основными) периодами T1 и T2 является функция с периодом НОК (T1,T2).
- Сумма 2 непрерывных функций с несоизмеримыми (даже основными) периодами является непериодической функцией.
- Не существует периодических функций, не равных константе, у которой периодами являются несоизмеримые числа.
Примеры
- Функция равная константе f(x) = const является периодической, и любое число является её периодом. Главного периода не имеет.
- Функция
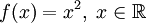 является апериоди́ческой.
является апериоди́ческой.
См. также
- Периодичность
- Квазипериодическая функция
Ссылки
Wikimedia Foundation. 2010.