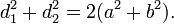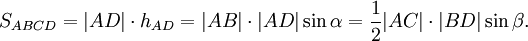Параллелограм

Параллелограмм

Параллелогра́мм (от греч. parallelos — параллельный и gramme — линия) — это четырёхугольник, у которого противолежащие стороны попарно параллельны, т. е. лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Свойства

• Противоположные стороны параллелограмма равны

  | AB | = | CD | , | AD | = | BC | .

• Противоположные углы параллелограмма равны

  $\angle A = \angle C, \angle B = \angle D.$

• Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам

  | AO | = | OC | , | BO | = | OD | .

• Сумма углов, прилежащих к одной стороне, равна 180°.
• Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон:

пусть а — длина стороны AB, b — длина стороны BC, d₁ и d₂ — длины диагоналей; тогда

$d_1^2+d_2^2 = 2(a^2 + b^2).$

Доказательства  

Проведя диагональ BD, мы получим два треугольника ABD и BCD, которые равны, т.к. одна сторона у них общая, а соответственные углы при стороне BD равны как накрест лежащие при параллельных прямых AB

• Аффинное преобразование всегда переводит параллелограмм в параллелограмм. Для любого параллелограмма существует аффинное преобразование, которое отображает его в квадрат.

Признаки параллелограмма

Четырёхугольник ABCD является параллелограммом, если выполняется одно из следующих условий:

1. Противоположные стороны попарно равны (|AB| = |CD|, |AD| = |BC|).
2. Противоположные углы попарно равны (∠A = ∠C, ∠B = ∠D).
3. Две противоположные стороны равны и параллельны (|AB| = |CD|, AB || CD).
4. Диагонали делятся в точке их пересечения пополам (|AO| = |OC|, |BO| = |OD|).

Площадь

Площадь параллелограмма S_ABCD можно найти по следующим формулам:

$S_{ABCD}=|AD|\cdot h_{AD}=|AB|\cdot |AD| \sin \alpha = \frac{1}{2} |AC|\cdot|BD|\sin \beta .$

где h_AD — высота опущенная на сторону AD, 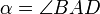$\alpha=\angle BAD$, β — угол между диагоналями.

См. также

• Трапеция
• Прямоугольник
• Ромб
• Дельтоид
• Параллелепипед
• Параллелограмм Вариньона