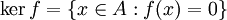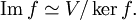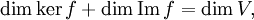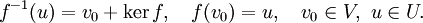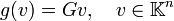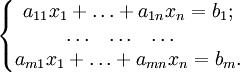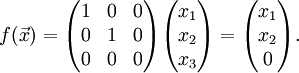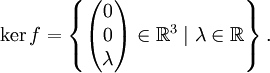Ядро линейного отображения
- Ядро линейного отображения
-
В различных разделах математики ядром отображения 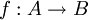 называется некоторое множество kerf, в некотором смысле характеризующее отличие f от инъективного отображения. Конкретное определение может различаться, однако для инъективного отображения f множество kerf всегда должно быть тривиально. Если множества A и B обладают некоторой структурой (например, являются группами или векторными пространствами), то kerf также должно обладать этой структурой, при этом различные формулировки основной теоремы о гомоморфизме связывают образ
называется некоторое множество kerf, в некотором смысле характеризующее отличие f от инъективного отображения. Конкретное определение может различаться, однако для инъективного отображения f множество kerf всегда должно быть тривиально. Если множества A и B обладают некоторой структурой (например, являются группами или векторными пространствами), то kerf также должно обладать этой структурой, при этом различные формулировки основной теоремы о гомоморфизме связывают образ 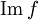 и фактормножество A / kerf.
и фактормножество A / kerf.
Ядро линейного отображения
Ядром линейного отображения  называется прообраз нулевого элемента пространства U:
называется прообраз нулевого элемента пространства U:
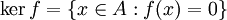
kerf является подпространством в V. Оно всегда содержит нулевой элемент пространства V. Согласно основной теореме о гомоморфизме, образ f изоморфен фактору пространства V по ядру f:
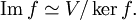
Соответственно, размерность образа пространства равна разности размерностей пространства и ядра отображения, если размерность V конечна:
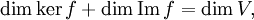
а прообраз любого вектора определён с точностью до прибавления вектора из ядра:
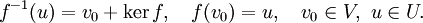
Теория матриц
Любую прямоугольную матрицу G размера 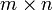 , содержащий элементы поля K (в частности, вещественные числа), можно рассматривать как линейный оператор
, содержащий элементы поля K (в частности, вещественные числа), можно рассматривать как линейный оператор 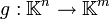 умножения векторов слева на матрицу:
умножения векторов слева на матрицу:
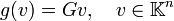
Таким образом, результаты теории конечномерных линейных пространств целиком переносятся на работу с матрицами. В частности, систему линейных уравнений с n неизвестными
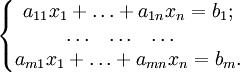
можно рассматривать как задачу поиска прообраза вектора 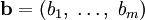 , а задача о решении однородной системы уравнений (
, а задача о решении однородной системы уравнений ( ) сводится к поиску ядра отображения g.
) сводится к поиску ядра отображения g.
Пример
Пусть f будет линейным отображением 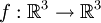 и:
и:
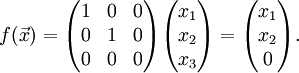
Тогда его ядро является векторным подпространством:
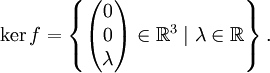
Гомоморфизм групп
Если f — гомоморфизм между группами, то kerf образует нормальную подгруппу A.
Гомоморфизм колец
Если f — гомоморфизм между кольцами, то kerf образует идеал кольца A.
Литература
- Винберг Э. Б. Курс алгебры. — 3-е изд. — Москва: Факториал Пресс, 2002. — 544 с. — 3000 экз. — ISBN 5-88688-060-7
См. также
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Ядро линейного отображения" в других словарях:
Ядро (алгебра) — У этого термина существуют и другие значения, см. Ядро. В различных разделах математики ядром отображения называется некоторое множество , в некотором смысле характеризующее отличие от инъективного отображения. Конкретное определение может… … Википедия
Ядро оператора — Линейным отображением (линейным оператором) векторного пространства LK над полем K в векторное пространство MK (над тем же полем K) называется отображение , удовлетворяющее условию линейности f(αx + βy) = αf(x) + βf(y). для всех и … Википедия
Линейные отображения — Линейным отображением (линейным оператором) векторного пространства LK над полем K в векторное пространство MK (над тем же полем K) называется отображение , удовлетворяющее условию линейности f(αx + βy) = αf(x) + βf(y). для всех и … Википедия
Линейное отображение — У этого термина существуют и другие значения, см. Отображение (значения). Линейное отображение, линейный оператор обобщение линейной числовой функции (точнее, функции ) на случай более общего множества аргументов и значений. Линейные… … Википедия
Линейное преобразование — Линейным отображением (линейным оператором) векторного пространства LK над полем K в векторное пространство MK (над тем же полем K) называется отображение , удовлетворяющее условию линейности f(αx + βy) = αf(x) + βf(y). для всех и … Википедия
Линейные операторы — Линейным отображением (линейным оператором) векторного пространства LK над полем K в векторное пространство MK (над тем же полем K) называется отображение , удовлетворяющее условию линейности f(αx + βy) = αf(x) + βf(y). для всех и … Википедия
Линейный оператор — Линейным отображением (линейным оператором) векторного пространства LK над полем K в векторное пространство MK (над тем же полем K) называется отображение , удовлетворяющее условию линейности f(αx + βy) = αf(x) + βf(y). для всех и … Википедия
Факторпространство по подпространству — Факторпространство по подпространству в линейной алгебре важный частный случай факторпространств. Содержание 1 Определение 2 Факторотображение … Википедия
Теоремы об изоморфизме — Запрос «Теорема об изоморфизме» перенаправляется сюда; см. также другие значения. Первая теорема об изоморфизме Т … Википедия
Формула произведения корангов — Формула произведения корангов математическая формула, выражающая коразмерность множества точек, в которых ядро производной отображения имеет заданную размерность, в виде произведения корангов данного отображения в прообразе и образе.… … Википедия
 называется некоторое множество kerf, в некотором смысле характеризующее отличие f от инъективного отображения. Конкретное определение может различаться, однако для инъективного отображения f множество kerf всегда должно быть тривиально. Если множества A и B обладают некоторой структурой (например, являются группами или векторными пространствами), то kerf также должно обладать этой структурой, при этом различные формулировки основной теоремы о гомоморфизме связывают образ
называется некоторое множество kerf, в некотором смысле характеризующее отличие f от инъективного отображения. Конкретное определение может различаться, однако для инъективного отображения f множество kerf всегда должно быть тривиально. Если множества A и B обладают некоторой структурой (например, являются группами или векторными пространствами), то kerf также должно обладать этой структурой, при этом различные формулировки основной теоремы о гомоморфизме связывают образ 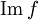 и фактормножество A / kerf.
и фактормножество A / kerf. называется прообраз нулевого элемента пространства U:
называется прообраз нулевого элемента пространства U: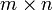 , содержащий элементы поля K (в частности, вещественные числа), можно рассматривать как линейный оператор
, содержащий элементы поля K (в частности, вещественные числа), можно рассматривать как линейный оператор 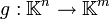 умножения векторов слева на матрицу:
умножения векторов слева на матрицу: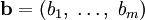 , а задача о решении однородной системы уравнений (
, а задача о решении однородной системы уравнений ( ) сводится к поиску ядра отображения g.
) сводится к поиску ядра отображения g.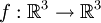 и:
и: