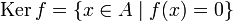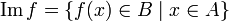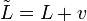- Линейные отображения
-
Лине́йным отображе́нием (лине́йным опера́тором) векторного пространства LK над полем K в векторное пространство MK (над тем же полем K) называется отображение
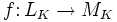 ,
,
удовлетворяющее условию линейности
- f(αx + βy) = αf(x) + βf(y).
для всех
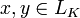 и
и 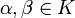 .
.Содержание
Важные частные случаи
- Линейный функционал — линейный оператор, для которого M = K:
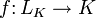
- Эндоморфизм — линейный оператор, для которого L = M:
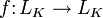
- Тождественный оператор — оператор
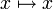 , отображающий каждый элемент пространства в себя.
, отображающий каждый элемент пространства в себя. - Нулевой оператор — оператор, переводящий каждый элемент LK в нулевой элемент MK.
- Сопряжённый оператор к оператору
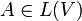 — оператор A * на V * , заданный соотношением (A * f,x): = (f,Ax).
— оператор A * на V * , заданный соотношением (A * f,x): = (f,Ax). - Эрмитов (самосопряжённый) оператор — оператор, совпадающий со своим сопряженным оператором. В случае евклидова пространства такой оператор называют еще симметричным.
Связанные понятия
- Ядром линейного отображения
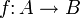 называются подмножество A, которое отображается в нуль:
называются подмножество A, которое отображается в нуль:
- Ядро линейного отображения образует подпространство в линейном пространстве A.
- Образом линейного отображения f называется следующее подмножество B:
- Образ линейного отображения образует подпространство в линейном пространстве B.
- Отображение
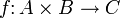 прямого произведения линейных пространств A и B в линейное пространство C называется билинейным, если оно линейно по обоим своим аргументам. Отображение прямого произведения большего числа линейных пространств
прямого произведения линейных пространств A и B в линейное пространство C называется билинейным, если оно линейно по обоим своим аргументам. Отображение прямого произведения большего числа линейных пространств 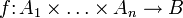 называется полилинейным, если оно линейно по всем своим аргументам.
называется полилинейным, если оно линейно по всем своим аргументам.
- Оператор
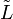 называется линейным неоднородным, если он имеет вид
называется линейным неоднородным, если он имеет вид
- где L — линейный оператор, а v — вектор.
Примеры
Примеры линейных однородных операторов:
-
- оператор дифференцирования:
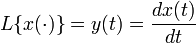 ;
; - оператор интегрирования:
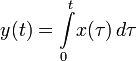 ;
; - оператор умножения на определённую функцию
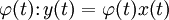 ;
; - оператор интегрирования с заданным «весом»
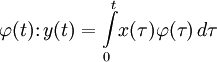
- оператор взятия значения функции f в конкретной точке x0: L{f} = f(x0);
- оператор умножения вектора на матрицу: b = Ax.
- оператор дифференцирования:
Примеры линейных неоднородных операторов:
-
- Любое аффинное преобразование;
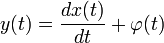 ;
;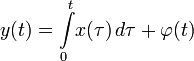 ;
;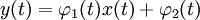 ;
;
где
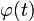 ,
, 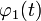 ,
, 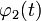 — вполне определённые функции, а x(t) — преобразуемая оператором функция.
— вполне определённые функции, а x(t) — преобразуемая оператором функция.См. также
- Вполне непрерывный оператор
- Интегральный оператор Фредгольма
- Разностный оператор
- Сопряжённый оператор
- Спектр оператора
- Оператор (математика)
- Выпуклый функционал
- Изометрический оператор
Wikimedia Foundation. 2010.