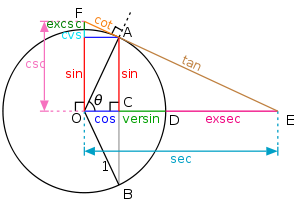
- Единичная окружность
-
Единичная окружность — это окружность с радиусом 1 и центром в начале координат. Понятие единичной окружности можно легко обобщить до n-мерного пространства (
 ). В таком случае используется термин «единичная сфера».
). В таком случае используется термин «единичная сфера».Для всех точек на окружности действительно согласно с теоремой Пифагора:
 .
.Не путайте термины «окружность» и «круг»!
- Окружность — геометрическое место точек, расположенное на данном расстоянии от данной точки, на одной плоскости — кривая.
- Круг — геометрическое место точек, расположенное не дальше чем окружность, на одной плоскости — фигура.
Содержание
Тригонометрические функции
Синус и косинус могут быть описаны следующим образом: соединив любую точку
 на единичной окружности с началом координат
на единичной окружности с началом координат  , мы получаем отрезок, находящийся под углом
, мы получаем отрезок, находящийся под углом  относительно положительной полуоси абсцисс. Тогда действительно:
относительно положительной полуоси абсцисс. Тогда действительно:Подставив эти значения в вышеуказанное уравнение
 , мы получаем:
, мы получаем:
Обратите внимание на общепринятое написание
 .
.Тут же наглядно описывается периодичность тригонометрических функций, так как угол отрезка не зависит от количества «полных оборотов»:
для всех целых чисел
 , иными словами,
, иными словами,  принадлежит
принадлежит  .
.Комплексная плоскость
В комплексной плоскости единичную окружность описывает множество
 :
:
Множество
 удоволетворяет условиям мультипликативной группы (с нейтральным элементом
удоволетворяет условиям мультипликативной группы (с нейтральным элементом  ).
).Ссылки
Этот раздел статьи ещё не написан. Согласно замыслу одного из участников Википедии, на этом месте должен располагаться специальный раздел.
Вы можете помочь проекту, написав этот раздел.См. также
- Единичная сфера
- Единичный квадрат
- Единичный куб
Категория:- Геометрические фигуры
Wikimedia Foundation. 2010.