Обратные тригонометрические функции

Обра́тные тригонометри́ческие фу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:

• аркси́нус (обозначение: arcsin)
• аркко́синус (обозначение: arccos)
• аркта́нгенс (обозначение: arctg; в иностранной литературе arctan)
• арккота́нгенс (обозначение: arcctg; в иностранной литературе arccot или arccotan)
• арксе́канс (обозначение: arcsec)
• арккосе́канс (обозначение: arccosec; в иностранной литературе arccsc)

Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arc — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Изредка в иностранной литературе пользуются обозначениями типа sin⁻¹ для арксинуса и т. п.; это считается не совсем корректным, так как возможна путаница с возведением функции в степень −1.

Основное соотношение

$\arcsin x + \arccos x = \frac{\pi}{2}$

$\operatorname {arctg}\, x + \operatorname {arcctg}\, x = \frac{\pi}{2}$

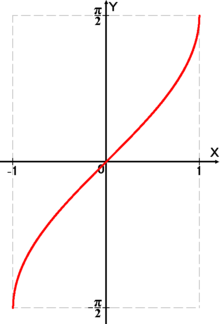
Функция arcsin

График функции $y = \arcsin x$.

Арксинусом числа m называется такое значение угла x, для которого $\sin x = m,\, -\frac{\pi}{2} \leqslant x \leqslant \frac{\pi}{2},\, |m|\leqslant 1.$

Функция $y=\sin x$ непрерывна и ограничена на всей своей числовой прямой. Функция $y=\arcsin x$ является строго возрастающей.

• $\sin (\arcsin x) = x\qquad$ при $-1 \leqslant x \leqslant 1,$
• $\arcsin(\sin y) = y\qquad$ при $-\frac{\pi}{2} \leqslant y \leqslant \frac{\pi}{2},$
• $D(\arcsin x)=[-1; 1]\qquad$ (область определения),
• $E(\arcsin x) = \left[-\frac{\pi}{2}; \frac{\pi}{2}\right]\qquad$ (область значений).

Свойства функции arcsin

• $\arcsin (-x) = -\arcsin x \qquad$ (функция является нечётной).
• $\arcsin x>0 \,$ при $0 < x \leqslant 1$.
• $\arcsin x = 0\,$ при $x=0.$
• $\arcsin x < 0\,$ при $-1 \leqslant x < 0.$
• $\arcsin x = \left\{\begin{matrix} \arccos \sqrt{1-x^2},\qquad 0 \leqslant x \leqslant 1 \\ -\arccos \sqrt{1-x^2},\qquad -1 \leqslant x \leqslant 0 \end{matrix}\right.$
• $\arcsin x = \operatorname{arctg} \frac{x}{\sqrt{1-x^2}}$
• $\arcsin x = \left\{\begin{matrix} \operatorname{arcctg}\, \frac{\sqrt{1-x^2}}{x},\qquad 0 < x \leqslant 1 \\ \operatorname{arcctg}\, \frac{\sqrt{1-x^2}}{x}-\pi,\qquad -1 \leqslant x < 0 \end{matrix}\right.$

Получение функции arcsin

Дана функция $y=\sin x.$ На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие $y= \arcsin x$ функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все значения области значений — $\left [ -\frac{\pi}{2}; \frac{\pi}{2} \right ]$. Так как для функции $y=\sin x$ на интервале $\left [ -\frac{\pi}{2}; \frac{\pi}{2} \right ]$ каждому значению аргумента соответствует единственное значение функции, то на этом отрезке существует обратная функция $y=\arcsin x,$ график которой симметричен графику функции $y=\sin x$ на отрезке $\left [ -\frac{\pi}{2}; \frac{\pi}{2} \right ]$ относительно прямой $y=x.$

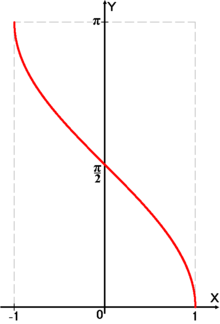
Функция arccos

График функции $y=\arccos x$.

Арккосинусом числа m называется такое значение угла x, для которого $\cos x = m,\qquad 0 \leqslant x \leqslant \pi, |m|\leqslant 1.$

Функция $y=\cos x$ непрерывна и ограничена на всей своей числовой прямой. Функция $y=\arccos x$ является строго убывающей.

• $\cos (\arccos x)=x$ при $-1 \leqslant x \leqslant 1,$
• $\arccos (\cos y) = y$ при $0 \leqslant y \leqslant \pi.$
• $D(\arccos x)=[-1; 1],$ (область определения),
• $E(\arccos x)=[0; \pi].$ (область значений).

Свойства функции arccos

• $\arccos(-x) = \pi - \arccos x\,$ (функция центрально-симметрична относительно точки $\left (0; \frac{\pi}{2}\right)$), является индифферентной.
• $\arccos x > 0\,$ при $-1 \leqslant x < 1.$
• $\arccos x = 0\,$ при $x=1.\,$
• $\arccos x = \left\{\begin{matrix} \arcsin \sqrt{1-x^2},\qquad 0 \leqslant x \leqslant 1 \\\pi-\arcsin \sqrt{1-x^2},\qquad -1 \leqslant x \leqslant 0 \end{matrix}\right.$
• $\arccos x = \left\{\begin{matrix} \operatorname{arctg}\, \frac{\sqrt{1-x^2}}{x},\qquad 0 < x \leqslant 1 \\\pi+\operatorname{arctg}\, \frac{\sqrt{1-x^2}}{x},\qquad -1 \leqslant x < 0 \end{matrix} \right.$
• $\arccos x = 2 \arcsin \sqrt \frac{1-x}{2}$
• $\arccos x = 2 \arccos \sqrt \frac{1+x}{2}$
• $\arccos x = 2 \operatorname{arctg} \sqrt \frac{1-x}{1+x}$

Получение функции arccos

Дана функция $y=\cos x.$ На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие $y=\arccos x$ функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго убывает и принимает все свои значения — $[0; \pi].$ На этом отрезке $y=\cos x$ строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке $[0; \pi]$ существует обратная функция $y = \arccos x,$ график которой симметричен графику $y=\cos x$ на отрезке $[0; \pi]$ относительно прямой $y=x.$

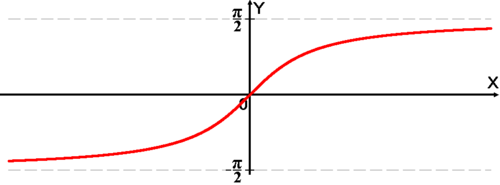
Функция arctg

График функции $y=\operatorname{arctg}\, x$.

Арктангенсом числа m называется такое значение угла $\alpha$, для которого $\operatorname{tg}\, \alpha = m , \qquad -\frac{\pi}{2} < \alpha < \frac{\pi}{2}.$

Функция $y=\operatorname{arctg} x$ непрерывна и ограничена на всей своей числовой прямой. Функция $y=\operatorname{arctg} x$ является строго возрастающей.

• $\operatorname{tg}\,(\operatorname{arctg}\, x)=x$ при $x \in \mathbb R,$
• $\operatorname{arctg}\,(\operatorname{tg}\, y)=y$ при $-\frac{\pi}{2}<y<\frac{\pi}{2},$
• $D(\operatorname{arctg}\,x) = (-\infty; \infty),$
• $E(\operatorname{arctg}\,x) = \left(-\frac{\pi}{2}; \frac{\pi}{2} \right)$

Свойства функции arctg

• $\operatorname{arctg} x = \arcsin \frac{x}{\sqrt{1+x^2}}$

• $\operatorname{arctg} x = \arccos \frac{1}{\sqrt{1+x^2}}$, при x > 0.

Получение функции arctg

Дана функция $y=\operatorname{tg}\, x.$ На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие $y=\operatorname{arctg}\, x$ функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз — $\left(-\frac{\pi}{2}; \frac{\pi}{2} \right).$ На этом отрезке $y=\operatorname{tg}\, x$ строго монотонно возрастает и принимает все свои значения только один раз, следовательно, на интервале $\left(-\frac{\pi}{2}; \frac{\pi}{2} \right)$ существует обратная $y=\operatorname{arctg}\, x$, график которой симметричен графику $y=\operatorname{tg}\,x$ на отрезке $\left(-\frac{\pi}{2}; \frac{\pi}{2} \right)$ относительно прямой $y=x.$

Функция arcctg

График функции y=arcctg x

Арккотангенсом числа m называется такое значение угла x, для которого $\operatorname{ctg}\,x = m,\qquad 0 < x < \pi.$

Функция $y=\operatorname{arcctg}\, x$ непрерывна и ограничена на всей своей числовой прямой. Функция $y=\operatorname{arcctg}\, x$ является строго убывающей.

• $\operatorname{ctg}\,(\operatorname{arcctg}\, x) = x$ при $x \in \mathbb R,$
• $\operatorname{arcctg}\,(\operatorname{ctg}\, y) = y$ при $0<y<\pi,$
• $D(\operatorname{arcctg}\, x) = (-\infty; \infty),$
• $E(\operatorname{arcctg}\, x) = (0; \pi).$

Свойства функции arcctg

• $\operatorname{arcctg}\, (-x) = \pi - \operatorname{arcctg}\, x$ (график функции центрально-симметричен относительно точки $\left(0; \frac{\pi}{2}\right).$
• $\operatorname{arcctg}\, x > 0$ при любых $x.$
• $\operatorname{arcctg}\, x = \left\{\begin{matrix} \arcsin \frac{1}{\sqrt{1+x^2}},\qquad x \geqslant 0 \\\pi-\arcsin \frac{1}{\sqrt{1+x^2}},\qquad x \leqslant 0\end{matrix}\right.$

Получение функции arcctg

Дана функция $y=\operatorname{ctg}\, x$. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие $y=\operatorname{arcctg}\, x$ функцией не является. Поэтому рассмотрим отрезок, на котором она строго убывает и принимает все свои значения только один раз — $(0; \pi)$. На этом отрезке $y=\operatorname{ctg}\, x$ строго убывает и принимает все свои значения только один раз, следовательно, на интервале $(0; \pi)$ существует обратная функция $y=\operatorname{arcctg}\, x$, график которой симметричен графику $y=\operatorname{ctg}\, x$ на отрезке $(0; \pi)$ относительно прямой $y=x.$ График симметричен к арктангенсу

Функция arcsec

$\mathop{\operatorname{arcsec}}\, (x)\, = \operatorname{arccos} \left( \frac{1}{x}\right)\,$

Функция arccosec

$\mathop{\operatorname{arccosec}}\, (x)\, = \operatorname{arcsin} \left( \frac{1}{x}\right)\,$

Производные от обратных тригонометрических функций

$(\arcsin x)' = \frac{1}{\sqrt{1-x^2}}.$
$(\arccos x)' = \frac{-1}{\sqrt{1-x^2}}.$
$(\operatorname{arctg}\, x)' = \frac{1}{\ 1+x^2}.$
$(\operatorname{arcctg}\, x)' = -\frac{1}{\ 1+x^2}.$

Интегралы от обратных тригонометрических функций

Неопределённые интегралы

Для действительных и комплексных x:

$\begin{align} \int \arcsin x\,dx &{}= x\,\arcsin x + \sqrt{1-x^2} + C,\\ \int \arccos x\,dx &{}= x\,\arccos x - \sqrt{1-x^2} + C,\\ \int \operatorname{arctg}\,x\,dx &{}= x\,\operatorname{arctg}\,x - \frac{1}{2}\ln\left(1+x^2\right) + C,\\ \int \operatorname{arcctg}\, x\,dx &{}= x\,\operatorname{arcctg}\, x + \frac{1}{2}\ln\left(1+x^2\right) + C,\\ \int \arcsec x\,dx &{}= x\,\arcsec x - \ln\left(x\left(1+\sqrt{{x^2-1}\over x^2}\,\right)\!\right) + C,\\ \int \operatorname{arccosec}\, x\,dx &{}= x\,\operatorname{arccosec}\, x + \ln\left(x\left(1+\sqrt{{x^2-1}\over x^2}\,\right)\!\right) + C. \end{align}$

Для действительных x ≥ 1:

$\begin{align} \int \arcsec x\,dx &{}= x\,\arcsec x - \ln\left(x+\sqrt{x^2-1}\right) + C,\\ \int \operatorname{arccosec}\, x\,dx &{}= x\,\operatorname{arccosec}\, x + \ln\left(x+\sqrt{x^2-1}\right) + C. \end{align}$

См. также Список интегралов от обратных тригонометрических функций

Интегралы от обратных тригонометрических функций

Неопределённые интегралы

Для действительных и комплексных x:

$\begin{align} \int \arcsin x\,dx &{}= x\,\arcsin x + \sqrt{1-x^2} + C,\\ \int \arccos x\,dx &{}= x\,\arccos x - \sqrt{1-x^2} + C,\\ \int \operatorname{arctg}\,x\,dx &{}= x\,\operatorname{arctg}\,x - \frac{1}{2}\ln\left(1+x^2\right) + C,\\ \int \operatorname{arcctg}\, x\,dx &{}= x\,\operatorname{arcctg}\, x + \frac{1}{2}\ln\left(1+x^2\right) + C,\\ \int \arcsec x\,dx &{}= x\,\arcsec x - \ln\left(x\left(1+\sqrt{{x^2-1}\over x^2}\,\right)\!\right) + C,\\ \int \operatorname{arccosec}\, x\,dx &{}= x\,\operatorname{arccosec}\, x + \ln\left(x\left(1+\sqrt{{x^2-1}\over x^2}\,\right)\!\right) + C. \end{align}$

Для действительных x ≥ 1:

$\begin{align} \int \arcsec x\,dx &{}= x\,\arcsec x - \ln\left(x+\sqrt{x^2-1}\right) + C,\\ \int \operatorname{arccosec}\, x\,dx &{}= x\,\operatorname{arccosec}\, x + \ln\left(x+\sqrt{x^2-1}\right) + C. \end{align}$

См. также Список интегралов от обратных тригонометрических функций

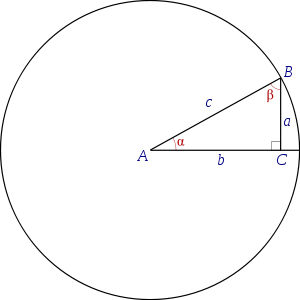
Использование в геометрии

Прямоугольный треугольник ABC

Обратные тригонометрические функции используются для вычисления углов треугольника, если известны его стороны, например с помощью теоремы косинусов.

В прямоугольном треугольнике, эти функции от отношений сторон сразу дают угол:

α = arcsin (a/c) = arccos (b/c) = arctg (a/b) = arccosec (c/a) = arcsec (c/b) = arcctg (b/a)

Связь с натуральным логарифмом

Для вычисления значений обратных тригонометрических функций от комплексного аргумента удобно использовать формулы, выражающие их через натуральный логарифм:

$\begin{align} \arcsin z & {}= -i \ln (iz+\sqrt{1-z^2}), \end{align}$

$\begin{align} \arccos z & {}= \dfrac{\pi}{2} + i \ln (iz+\sqrt{1-z^2}), \end{align}$

$\begin{align} \operatorname{arctg}\,z & {}= \dfrac{i}{2} ( \ln(1-iz)-\ln(1+iz) ), \end{align}$

$\begin{align} \operatorname{arcctg}\,z & {}= \dfrac{i}{2} \left( \ln \left( \dfrac{z-i}{z} \right)-\ln \left( \dfrac{z+i}{z} \right) \right), \end{align}$

$\begin{align} \arcsec z & {}= \arccos\left(z^{-1}\right) = \dfrac{\pi}{2} + i \ln \left( \sqrt{1-\dfrac{1}{z^2}} + \dfrac{i}{z} \right), \end{align}$

$\begin{align} \operatorname{arccosec}\,z & {}= \arcsin\left(z^{-1}\right) = - i \ln \left( \sqrt{1-\dfrac{1}{z^2}} + \dfrac{i}{z} \right). \end{align}$

См. также

• Тригонометрические функции
• Обратные гиперболические функции
• Теорема Данжуа — Лузина

Ссылки

• Weisstein, Eric W. Обратные тригонометрические функции (англ.) на сайте Wolfram MathWorld.
• Обратные тригонометрические функции — статья из Большой советской энциклопедии
• Построение графиков обратных тригонометрических функций онлайн
• Онлайн калькулятор: обратные тригонометрические функции