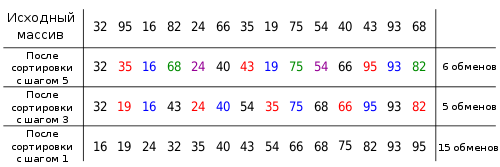Сортировка Шелла

Сортировка Шелла (англ. Shell sort) — алгоритм сортировки, являющийся усовершенствованным вариантом сортировки вставками. Идея метода Шелла состоит в сравнении элементов, стоящих не только рядом, но и на определённом расстоянии друг от друга. Иными словами — это сортировка вставками с предварительными «грубыми» проходами. Аналогичный метод усовершенствования пузырьковой сортировки называется сортировка расчёской.

Описание

При сортировке Шелла сначала сравниваются и сортируются между собой значения, отстоящие один от другого на некотором расстоянии $d$ (о выборе значения $d$ см. ниже). После этого процедура повторяется для некоторых меньших значений $d$, а завершается сортировка Шелла упорядочиванием элементов при $d=1$ (то есть обычной сортировкой вставками). Эффективность сортировки Шелла в определённых случаях обеспечивается тем, что элементы «быстрее» встают на свои места (в простых методах сортировки, например, пузырьковой, каждая перестановка двух элементов уменьшает количество инверсий в списке максимум на 1, а при сортировке Шелла это число может быть больше).

Невзирая на то, что сортировка Шелла во многих случаях медленнее, чем быстрая сортировка, она имеет ряд преимуществ:

• отсутствие потребности в памяти под стек;
• отсутствие деградации при неудачных наборах данных — быстрая сортировка легко деградирует до O(n²), что хуже, чем худшее гарантированное время для сортировки Шелла.

История

Сортировка Шелла была названа в честь её изобретателя — Да Шелла, который опубликовал этот алгоритм в 1959 году.

Пример

Пусть дан список $A = (32, 95, 16, 82, 24, 66, 35, 19, 75, 54, 40, 43, 93, 68)$ и выполняется его сортировка методом Шелла, а в качестве значений $d$ выбраны $5, 3, 1$.

На первом шаге сортируются подсписки $A$, составленные из всех элементов $A$, различающихся на 5 позиций, то есть подсписки $A_{5,1} = (32, 66, 40)$, $A_{5, 2} = (95, 35, 43)$, $A_{5, 3} = (16, 19, 93)$, $A_{5, 4} = (82, 75, 68)$, $A_{5, 5} = (24, 54)$.

В полученном списке на втором шаге вновь сортируются подсписки из отстоящих на 3 позиции элементов.

Процесс завершается обычной сортировкой вставками получившегося списка.

Выбор длины промежутков

Среднее время работы алгоритма зависит от длин промежутков — $d$, на которых будут находиться сортируемые элементы исходного массива ёмкостью $N$ на каждом шаге алгоритма. Существует несколько подходов к выбору этих значений:

• первоначально используемая Шеллом последовательность длин промежутков: $~d_1 = N/2, d_i = d_{i-1} / 2, d_k = 1$ в худшем случае, сложность алгоритма составит $O( N^2 )$;
• предложенная Хиббардом последовательность: все значения $~2^i-1 \le N, i \in \mathbb N$; такая последовательность шагов приводит к алгоритму сложностью $O(N^{3/2})$;
• предложенная Седжвиком последовательность: $~d_i = 9\cdot2^i - 9\cdot2^{i/2} + 1$, если i четное и $~d_i = 8\cdot2^i - 6\cdot2^{(i+1)/2} + 1$, если i нечетное. При использовании таких приращений средняя сложность алгоритма составляет: $O(n^{7/6})$, а в худшем случае порядка $O(n^{4/3})$. При использовании формулы Седжвика следует остановиться на значении inc[s-1], если 3*inc[s] > size.^[1];
• предложенная Праттом последовательность: все значения $~2^i\cdot3^j \le N/2, i, j \in \mathbb N$; в таком случае сложность алгоритма составляет $O(N (log N)^2)$;
• эмпирическая последовательность Марцина Циура (последовательность A102549 в OEIS): $~d \in \left\{1, 4, 10, 23, 57, 132, 301, 701, 1750\right\}$; является одной из лучших для сортировки массива ёмкостью приблизительно до 4000 элементов.^[2];
• эмпирическая последовательность, основанная на числах Фибоначчи: $~d \in \left\{F_n\right\}$;
• все значения $~(3^j-1)/2 \le N/2$ ^{[источник не указан 1119 дней]}, $j \in \mathbb N$; такая последовательность шагов приводит к алгоритму сложностью $O(N^{3/2})$.

Примечания

1. ↑ J. Incerpi, R. Sedgewick, «Improved Upper Bounds for Shellsort», J. Computer and System Sciences 31, 2, 1985.
2. ↑ Marcin Ciura Best Increments for the Average Case of Shellsort

Ссылки

Имеется викиучебник по теме
«Примеры реализации сортировки Шелла»

• Д. Кнут. Искусство программирования. Том 3. Сортировка и поиск, 2-е изд. Гл. 5.2.1. ISBN 5-8459-0082-4
• Анимированное представление алгоритма сортировки Шелла
• Представление алгоритма сортировки Шелла в виде танца (видео)