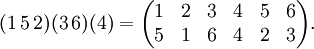- Инверсия (перестановка)
-
Перестано́вка — это упорядоченный набор чисел
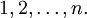 При этом n называется порядком перестановки. Число всех перестановок порядка n равно
При этом n называется порядком перестановки. Число всех перестановок порядка n равно 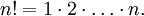
Более общо, перестановкой произвольного (хотя обычно конечного) множества X называется биекция
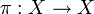 .
.Содержание
Свойства
- Композиция определяет операцию произведения на перестановках
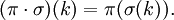 Относительно этой операции множество перестановок образует группу, которую называют симметрической и обычно обозначают Sn (n — количество переставляемых элементов).
Относительно этой операции множество перестановок образует группу, которую называют симметрической и обычно обозначают Sn (n — количество переставляемых элементов). - Любая группа является подгруппой группы перестановок некоторого множества (например множества элементов этой группы). Каждый элемент
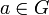 сопоставляется с перестановкой
сопоставляется с перестановкой 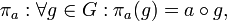 где
где  — операция в группе G.
— операция в группе G.
Связанные определения
- Носитель перестановки
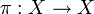 — это подмножество множества X, определяемое как
— это подмножество множества X, определяемое как 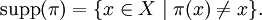
- Неподвижной точкой перестановки π является всякая неподвижная точка отображения
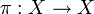 , то есть элемент множества
, то есть элемент множества 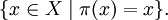 Множество всех неподвижных точек перестановки π является дополнением её носителя в X.
Множество всех неподвижных точек перестановки π является дополнением её носителя в X. - Инверсией в перестановке π порядка n называется всякая пара индексов i, j такая, что
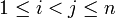 и π(i) > π(j). Чётность числа инверсий в перестановке определяет чётность перестановки.
и π(i) > π(j). Чётность числа инверсий в перестановке определяет чётность перестановки.
Специальные типы перестановок
- Инволюция — перестановка τ, которая является обратной самой себе, то есть
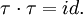
- Беспорядок — перестановка без неподвижных точек.
- Циклом длины
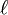 называется такая подстановка π, которая тождественна на всём множестве X, кроме подмножества
называется такая подстановка π, которая тождественна на всём множестве X, кроме подмножества 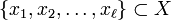 и
и 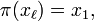 π(xi) = xi + 1. Обозначается
π(xi) = xi + 1. Обозначается 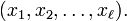
- Транспозиция — перестановка элементов множества X, которая меняет местами два элемента. Транспозиция является циклом длины 2.
Подстановки и произведения циклов
Перестановка π множества X может быть записана в виде подстановки, например:
где
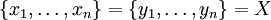 и π(xi) = yi.
и π(xi) = yi.Перестановку также можно записать в виде произведения непересекающихся циклов, причем единственным образом с точностью до порядка следования циклов в произведении. Например:
Случайная перестановка
Случайной перестановкой называется называется случайный вектор ξ = (ξ1,...,ξn), все элементы которого принимают натуральные значения от 1 до n, и при этом вероятность совпадения любых двух элементов равна 0.
Независимой случайной перестановкой называется такая случайная перестановка ξ, для которой
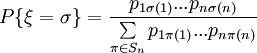 для некоторых pij, для которых
для некоторых pij, для которых 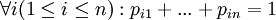 и
и 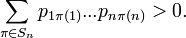 Если при этом pij не зависят от i, то перестановку ξ называют одинаково распределённой. Если же нет зависимости от j, то есть
Если при этом pij не зависят от i, то перестановку ξ называют одинаково распределённой. Если же нет зависимости от j, то есть 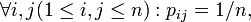 то ξ называют однородной.
то ξ называют однородной.См. также
- Чётность перестановки (англ.)
- Гигантская компонента
- Композиция определяет операцию произведения на перестановках
Wikimedia Foundation. 2010.