Лемма Шпернера

Лемма Шпернера — комбинаторный аналог теоремы Брауэра о неподвижной точке, один из основных результатов комбинаторной топологии. Утверждает, что при любой Шпернеровсокй раскраске вершин в триангуляции n-мерного симплекса найдётся ячейка триангуляции, вершины которой поскрашены во все цвета. Первый результат подобного типа был доказан Эмануэлем Штернером.

Одномерный случай

В одномерном случае, лемма Шпернера может рассматриваться как дискретный аналог теоремы Больцано — Коши. Она утверждает, что если большой отрезок разбит на подотрезки и в вершинах отрезков расставлены единицы и двойки, то при условии, что в вершинах большого отрезка стоят разные значения, существует отрезок подразбиения, в вершинах которого стоят разные значения.

Двумерный случай

Двумерный случай

Этот вариант является самым распространённым. Формулируется он следующим образом:

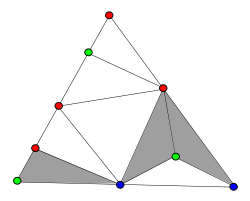
Дан треугольник, вершины которого помечены цифрами 0, 1 и 2, и его триангуляция. Вершины триангуляции пометили теми же значениями таким образом, чтобы любая вершина на стороне исходного треугольника была бы помечена одной из пометок вершин этой стороны. Тогда обязательно существует треугольник разбиения, помеченный цифрами 0, 1, 2.

Многомерный случай

В общем случае лемма касается триагуляции n-мерного симплекса

$\mathcal{A}=A_1 A_2 \ldots A_{n+1}.$

Рассмотрим его триангуляцию T, являющуюся разбиением $\mathcal{A}$ на меньшие n-мерные симплексы. Обозначим функцию цвета вершины за f : S → {1,2,3,...,n,n+1}, где S обозначает множество вершин триангуляции T. Расскраска называется Шпернеровской, если выполнены следующие правила:

1. Вершины большого симплекса поскрашены в разные цвета, то есть. f(A_i) = i for 1 ≤ i ≤ n+1.
2. Те вершины T, что лежат в одной k-мерной грани большого симплекса

$A_{i_1}A_{i_2}\ldots A_{i_k}$

покрашены в цвета образующих её вершин

$f(A_{i_1}),f(A_{i_2}),\ldots,f(A_{i_k}).$

В случае, если расскраска оказалась Шпернеровской, существует симплекс триангуляции T, вершины которого покрашены во все цвета.

Доказательство

В то время, как одномерный случай очевиден, мы докажем двумерный случай, предварительно обобщив утверждение. Доказательство многомерного случая получается аналогичным образом по индукции.

Рассмотрим граф G, постороенный по триангуляции T следующим образом:

Вершинами G будут треугольники T и область за пределами большого треугольника.

Две вершины соединим ребром, если соответствующие им области имееют общий отрезок, вершины которого покрашены в 1 и 2. На стороне, соединяющей две вершины большого треугольника, покрашенные в 1 и 2, есть нечётное число отрезков с вершинами 1 и 2, а значит степень вершины, соответствующей внешней области нечётна. Так как в графе должно быть чётное число вершин нечётной степени, то существует нечётное число (а значит хотя бы одна) вершин нечётной степени, соответствующих треугольникам T.

Легко проверить, что возможные степени вершин, соответствующих треугольникам, это 0, 1 или 2, и 1 соответствует треугольнику, вершины которого покрашены во все три цвета.

В многомерном случае нужно точно так же доказывать существование нечётного числа симплексов разбиения, вершины которых раскрашены во все цвета.

Литература

• Шашкин Ю. А. Неподвижные точки. — Москва: Наука, 1989. — 80 с. — (Популярные лекции по математике). — ISBN 5-02-013922-X

См. также

• Теорема Брауэра о неподвижной точке
• Теорема Борсука — Улама

Ссылки

• Доказательство леммы (англ.) на сайте Cut-The-Knot (англ.)

Для улучшения этой статьи желательно?: Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное. Викифицировать статью.