Лемма о рукопожатиях

Чётное число вершин (четыре: 2, 4, 5 и 6) данного графа имеют нечётную степень. Сумма степеней всех вершин равна 14, то есть удвоенному числу рёбер графа.

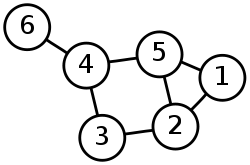
Лемма о рукопожатиях — положение теории графов, согласно которому любой конечный неориентированный граф имеет чётное число вершин нечётных степеней. Лемма берёт название от популярной аналогии: в группе людей, некоторые из которых пожимают друг другу руки, чётное число людей поприветствовало таким образом нечётное число коллег.

Лемма является следствием формулы суммы степеней, также иногда называемой леммой о рукопожатиях.

$\sum_{v\in V} \deg(v) = 2|E|$

для графа с множеством вершин V и множеством рёбер E. Оба результата доказаны Эйлером в его знаменитом докладе о семи мостах Кёнигсберга (1736). Эта работа положила начало исследованиям в области теории графов.

Вершины нечётных степеней графа иногда называются нечётными узлами или нечётными вершинами. Используя эту терминологию, можно перефразировать лемму таким образом: каждый граф имеет чётное число нечётных вершин.

Доказательство

При доказательстве упомянутой формулы Эйлер использовал технику двойного (повторного) счёта. Он посчитал количество инцидентных пар (v,e), где e — ребро и v — одна из его концевых вершин двумя разными способами. Вершина v принадлежит парам deg(v), где deg(v) — степень вершины (количество инцидентных ей рёбер). Следовательно, число инцидентных пар совпадает с суммой всех степеней. Однако каждое ребро принадлежит двум инцидентным парам, так как имеет две концевые вершины. Поэтому число инцидентных пар равно 2|E|. Поскольку две данные формулы предназначены для одного и то же множества, их значения одинаковы.

Чётность или нечётность суммы целых чисел не зависит от количества чётных слагаемых. Сумма чётна, если число нечётных слагаемых чётно (и нечётна в противном случае). Так как одна часть уравнения всегда чётна (2|E|), другая часть должна содеражать чётное число нечётных слагаемых, т. е. вершин нечётной степени.

Регулярные графы

Формулы суммы степеней подразумевает, что k-регулярный граф с числом вершин n имеет kn/2 рёбер.^[1] В частности, если k нечётно, число рёбер должно делиться на k.

Бесконечные графы

Лемма не применима к бесконечным графам, даже если они имеют конечное число нечётных вершин. Например, бесконечный путь с одной концевой вершиной имеет единственную нечётную вершину (то есть, нечётное количество).

Графы обмена

Этот раздел статьи ещё не написан. Согласно замыслу одного из участников Википедии, на этом месте должен располагаться специальный раздел. Вы можете помочь проекту, написав этот раздел.

Вычислительная сложность

Этот раздел статьи ещё не написан. Согласно замыслу одного из участников Википедии, на этом месте должен располагаться специальный раздел. Вы можете помочь проекту, написав этот раздел.

Другие приложения

Лемма о рукопожатиях также использована при доказательстве леммы Шпернера и кусочно-линейного случая проблемы «о восхождении на гору».

Примечания

1. ↑ Олдес, Джоан M. & Уилсон, Робин Дж. (2000), "Theorem 2.2", «Graphs and Applications: an Introductory Approach», Undergraduate Mathematics Series, The Open University, Springer-Verlag, с. 44, ISBN 978-1-85233-259-4 

Источники

• Кэмерон, Кэти & Эдмондс, Джек (1999), "«Some graphic uses of an even number of odd nodes»", Annales de l'Institut Fourier Т. 49 (3): 815–827, <http://www.numdam.org/item?id=AIF_1999__49_3_815_0> .
• Эйлер, Л. (1736), "«Solutio problematis ad geometriam situs pertinentis»", Commentarii Academiae Scientiarum Imperialis Petropolitanae Т. 8: 128–140, <http://math.dartmouth.edu/~euler/docs/originals/E053.pdf> . Печать и перевод: Биггз, Н. Л.; Лойд, И. K. & Уилсон, Р. Дж. (1976), «Graph Theory 1736–1936», Oxford University Press .
• Пападимитриу, Христос Х. (1994), "«On the complexity of the parity argument and other inefficient proofs of existence»", Journal of Computer and System Sciences Т. 48 (3): 498–532, DOI 10.1016/S0022-0000(05)80063-7 .
• Томасон, A. Дж. (1978), "Hamiltonian cycles and uniquely edge colourable graphs", «Advances in Graph Theory (Cambridge Combinatorial Conf., Trinity College, Cambridge, 1977)», vol. 3, Annals of Discrete Mathematics, сс. 259–268, DOI 10.1016/S0167-5060(08)70511-9 .