ШПЕРНЕРА ЛЕММА

если покрытие замкнутого n-мерного симплекса Т ⁿ состоит из п+1 залмкнутых множеств А ₀, A₁,..., А _п, поставленных в соответствие вершинам а ₀, а ₁, ..., а _п симплекса Т ⁿ таким образом, что каждая грань 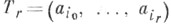этого симплекса покрыта множествами 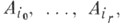соответствующими ее вершинам, то существует точка, принадлежащая всем множествам А ₀, A₁,..., А _п. Установлена Э. Шпернером (см. [1]). Из Ш. л. следует, что Лебега размерность пространства 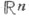есть п. Ш. л. используется также для доказательства Брауэра теорем о неподвижной точке и об инвариантности области.

Лит.:[1] Sperner E., лAbh. Math. Sem. Hamb.