Пуассоновский процесс

Пуассоновский процесс

Пуассо́новский проце́сс в теории случайных процессов описывает количество наступивших случайных событий, происходящих с постоянной интенсивностью.

Определение

Различают два вида Пуассоновского процесса: простой (или просто: Пуассоновский процесс) и сложный (обобщённый).

Простой Пуассоновский процесс

Пусть λ > 0. Случайный процесс 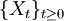$\{X_t\}_{t \ge 0}$ называется однородным Пуассоновским процессом с интенсивностью λ, если

1. X₀ = 0 почти наверное.
2. {X_t} — процесс с независимыми приращениями.
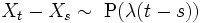3. $X_t - X_s \sim \ \mathrm{P}(\lambda(t-s))$ для любых 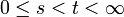$0 \le s < t < \infty$, где P(λ(t − s)) обозначает распределение Пуассона с параметром λ(t − s).

Сложный (обобщённый) Пуассоновский процесс

• Пусть ξ₁,...,ξ_n последовательность взаимно независимых одинаково распределённых случайных величин.
• Пусть N(t) - простой Пуассоновский процесс с интенсивностью λ, не зависящий от последовательности ξ₁,...,ξ_n.

Обозначим через S_k cумму первых k элементов введённой последовательности.

Тогда определим сложный Пуассоновский процесс {Y_t} как S_N(t) .

Свойства

• Пуассоновский процесс принимает только неотрицательные целые значения, и более того

$\mathbb{P}(X_t = k) = \frac{\lambda^k t^k}{k!} e^{-\lambda t}, \quad k = 0,1,2,\ldots$.

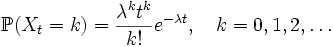• Траектории Пуассоновского процесса — кусочно-постоянные, неубывающие функции со скачками равными единице почти наверное. Более точно

$\mathbb{P}(X_{t+h} - X_t = 0) = 1-\lambda h + o(h)$

$\mathbb{P}(X_{t+h} - X_t = 1) = \lambda h + o(h)$

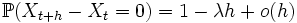
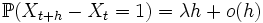
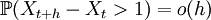$\mathbb{P}(X_{t+h} - X_t > 1) = o(h)$ при $h \to 0$,

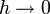где o(h) обозначает «о малое».

• Пуассоновский процесс стационарен.

Критерий

Для того чтобы некоторый случайный процесс {X_t} с непрерывным временем был Пуассоновским (простым, однородным) или тождественно нулевым достаточно выполнение следующих условий:

1. X₀ = 0.
2. Процесс имеет независимые приращения.
3. Процесс однородный.
4. Процесс принимает целые неотрицательные значения.
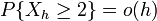5. $P\{X_h \geq 2\} = o(h)$ при $h \searrow 0$.

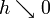Информационные свойства

• Пусть 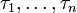$\tau_1,\dots,\tau_n$ — моменты скачков пуассоновского процесса. T = τ_j − τ_{j − 1}.
  

Зависит ли T от предыдущей части траектории?
$\mathbb P(\{T>t+s \mid T>s\})$ — ?

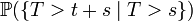Пусть $u(t)= \mathbb P(T>t)$.

$u(t\mid s)=\frac{ \mathbb P(T>t+s\cap T>s)}{ \mathbb P(T>s)}=\frac{\mathbb P(T>t+s)}{\mathbb P(T>s)}$
$u(t\mid s)u(s)=u(t+s)$
$u(t\mid s)=s(t) \Leftrightarrow u(t)=e^{-\alpha t}$.
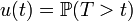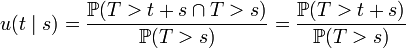
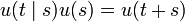
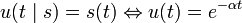Распределение длин промежутков времени между скачка́ми обладает свойством отсутствия памяти ⇔ оно показательно.

• Рассмотрим отрезок [a,b] на временно́й оси.
  

X(b) − X(a) = n — число скачков на отрезке [a,b].
Условное распределение моментов скачков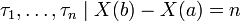 $\tau_1,\dots,\tau_n\mid X(b)-X(a)=n$ совпадает с распределением вариационного ряда, построенного по выборке длины n из R[a,b].

Плотность этого распределения $f_{\tau_1,\dots,\tau_n}(t)=\frac{n!}{(b-a)^n}\mathbb{I}(t_j\in[a,b]\ \forall j=\overline{1,n})$

ЦПТ

• Теорема.
  

$\mathbb P\biggl(\frac{X(t)-\lambda t}{\sqrt{ \lambda t}}< x\biggr)\underset{\lambda t\to\infty}{\overset x\rightrightarrows}\Phi(x)\sim N(0,1)=\frac1{\sqrt{2\pi}}\int_{-\infty}^xe^{-\frac{u^2}2}du$

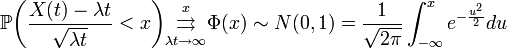
Скорость сходимости:
$\sup\limits_x\biggl|\mathbb P \biggl(\frac{X(t)-\lambda t}{\sqrt{\lambda t}}< x \biggr)-\Phi(x)\biggr| \leqslant\frac{C_0}{\sqrt{ \lambda t}}$,
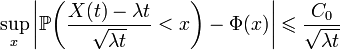где C₀ — константа Берри-Эссеена.

Применение

Для построения моделей различных систем обслуживания и анализа пригодности их дисциплин часто применяют Пуассоновский процесс. Так же возможно применение для анализа финансовых механизмов, таких как поток платежей и пр.