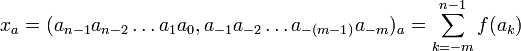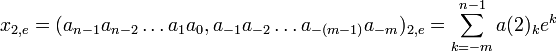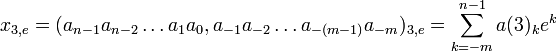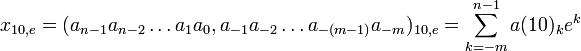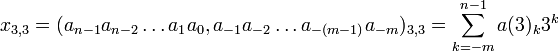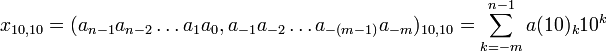- Комбинированная система счисления
-
Комбинированная система счисления
В комбинированных системах счисления для записи чисел используются две или более систем счисления с разными основаниями. В общем случае возможно бесконечное множество комбинированных систем счисления.
В спаренных (сдвоенных, двойных) системах счисления используются две системы счисления.
В строенных (тройных) системах счисления используются три системы счсления.
В счетверённых (четверных) системах счисления используются четыре системы счисления.Одинарные системы счисления
являются простыми (некомбинироваными) непозиционными системами счисления. В общем случае могут быть суммы, произведения, возведения в степень и другие функции от функций f(ak),
но наибольшее распространение получили системы счисления с суммированием функций от ak,
n — число разрядов целой части числа,
m — число разрядов дробной части числа, от 0 до бесконечности, при m=0 числа — целые,
k — число от -m до n-1, номер разряда,
a — основание основной внутриразрядной системы счисления,
ak — числа в разрядах из замкнутого множества a, цифры представляемого числа — xaпри f(ak)=ak образуется непозиционная система счисления с единичным весовым коэффициентом во всех разрядах,
при f(ak)=akak образуются показательные позиционные системы счисления с основанием a,
при m=0 и ak=1 образуется непозиционная унарная система счисления,
при добавлении межразрядной функции во второй вспомогательной межразрядной системе счисления с основанием b — f(b, k), чаще всего в виде сомножителя, но могут быть и другие зависимости, образуются комбинированные сдвоенные системы счисления.
Сдво́енные системы счисления
Представляемое число x(a, b) может быть записано в виде строки цифр с разделителями и индексами, что не полностью определяет число x(a, b), так как в такой записи нет весовых коэффициентов — f(b, k), которые подразумеваются, или может быть записано в виде суммы произведений, обозначающей полином, что тоже не полностью определяет число x(a, b), так как в такой записи отсутствуют цифры числа. Объединение обеих записей — строки и суммы полностью определяет число x(a, b), но местами избыточно и плохо вписывается в строку текста.
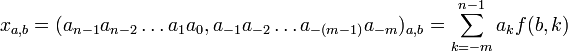 , где:
, где:
b — число, основание вспомогательной межразрядной системы счисления,
f(b, k) — числа межразрядной функции, весовые коэффициенты,
если межрязрядная функция является показательной f(b, k)=bk, то образуются показательные позиционные системы счисления с суммированием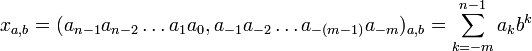 , для которых существует теорема Джона фон Неймана о экономичности позиционных показательных (a,b)-ичных систем счисления[1],
, для которых существует теорема Джона фон Неймана о экономичности позиционных показательных (a,b)-ичных систем счисления[1],
при m=0 образуются целые числа:
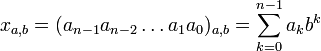 , которые являются частями степенного ряда (число есмь ряд):
, которые являются частями степенного ряда (число есмь ряд):
в котором коэффициенты an берутся из некоторого кольца
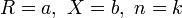 , а верхний предел ограничен с
, а верхний предел ограничен с 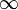 до числа цифр в числе - n-1,
до числа цифр в числе - n-1,если межразрядная функция не зависит от номера разряда — k, f(b, k)=f(b), то образуются одинарные (простые, несдвоенные) непозиционные системы счисления,
если основание множества a, из которого берутся ak, равно основанию межразрядной системы счисления b, то образуются (a,a)-ичные системы счисления, которые часто называют b-ричными системами счисления.
Сдвоенные позиционные показательные двоичные системы счисления
при ak из a={0,1} и b=2 образуется (2,2)-ичная (обычная) двоичная система счисления:
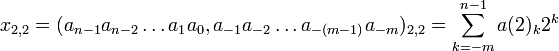 , при m=0 образуются целые (2,2)-ичные (обычные двоичные) числа:
, при m=0 образуются целые (2,2)-ичные (обычные двоичные) числа: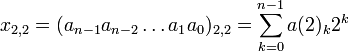 ,
,которые являются частичными (частными) суммами степенного ряда:
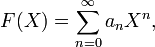 в котором коэффициенты an берутся из кольца R=a={0,1}, X=2, n=k, а верхний предел в частных суммах ограничен с
в котором коэффициенты an берутся из кольца R=a={0,1}, X=2, n=k, а верхний предел в частных суммах ограничен с 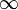 до n-1.
до n-1.Число представимых чисел в позиционных системах счисления
Количество чисел, которое можно представить в системе счисления, с основанием a, равно na, где n - число используемых разрядов.
Однако, кроме этого можно оценить «экономичность» системы счисления. Предположим, что нам нужно отобразить с помощью карточек на экране трёхзначное число. В двоичной системе нам нужно 2 * 3 = 6 карточек, при этом мы сможем показать 23 = 8 различных чисел. Если карточек меньше, то мы не сможем показать числа 010 = 0002 или 710 = 1112.
Пусть
- a - основание системы счисления
- n - число разрядов
- z = n * a - количество карточек, использованных для представления всех различных чисел по данному основанию с данным количеством разрадов
- na - количество представимых чисел
Теперь если мы выразим количество представимых чисел na от количества знаков n * a, мы и получим экономичность системы. Теперь можно также показать, какая система счисления наиболее экономичная.
Удельное натуральнологарифмическое число представимых чисел
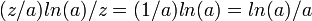 .
.Необходимыми условиями существования экстремума функции являются существование первой производной и её равенство нулю. Первая производная функции
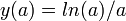 равна
равна 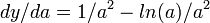 , т.е. существует. Приравняв её нулю
, т.е. существует. Приравняв её нулю 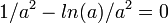 ,
, 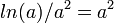 ,
, 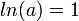 , получим
, получим  .
.
Достаточными условиями существования локального максимума являются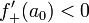 и
и 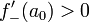 . Так как слева от точки a=e производная положительная, а справа отрицательная, то, в точке a=е=2,71... функция действительно имеет строгий локальный максимум.
. Так как слева от точки a=e производная положительная, а справа отрицательная, то, в точке a=е=2,71... функция действительно имеет строгий локальный максимум.
Из формулы и графика следует, что:
1. наибольшим удельным натуральнологарифмическим числом представимых чисел обладают системы счисления с внутриразрядным основанием - a=e=2,71...,
2. из целочисленных систем счисления наибольшим удельным натуральнологарифмическим числом представимых чисел обладают системы счисления с основанием a=3, системы счисления с основаниями a=2 и a=4 делят второе место.
3. при дальнейшем увеличении основания a системы счисления (более 4) удельное натуральнологарифмическое число представимых чисел ещё более уменьшается.Плотность записи чисел в позиционных системах счисления
Если число представимых чисел от основания весовой функции - b и вида весовой функции - f(k)=b(k) не зависит, то диапазон представимых чисел и плотность записи чисел зависят и от основания весовой функции - b и от вида весовой функции - f(k)=b(k).
Сдвоенные позиционные показательные е-ричные системы счисления
Из показательных позиционных систем счисления наибольшим удельным натуральнологарифмическим числом представимых чисел обладают (e,b)-ричные системы счисления с основанием равным числу Эйлера (е=2,71…).[1](§ 14. Об одном замечательном свойстве троичной системы. Стр.37-40.)
Применение (e,b)-ричных систем счисления в настоящее время затруднительно из-за отсутствия триггеров с нецелочисленным числом устойчивых состояний, но на целочисленных эвм возможно применение комбинированных (2,e)-ричной, (3,e)-ричной, (10,e)-ричной и других (a,е)-ричных систем счисления.
При ak из a={0,1} и b=е=2,71… образуется (2,e)-ричная система счисления:(2,е)-ричная система счисления хорошо подходит для вычислений в (2,е)-ричной системе счисления на двоичных эвм,
при m=0 образуются "(2,е)-целые" числа: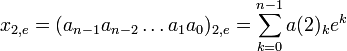 , которые являются частями (частичными суммами или частными суммами [2](стр.533)) степенного ряда (так как число Эйлера является суммой ряда
, которые являются частями (частичными суммами или частными суммами [2](стр.533)) степенного ряда (так как число Эйлера является суммой ряда 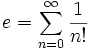 , то (2,е)-ричное число есмь ряд рядов):
, то (2,е)-ричное число есмь ряд рядов):
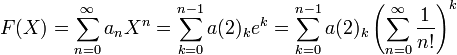 ,
,
в котором коэффициенты an берутся из кольца R={0,1}, X=e, n=k, а верхний предел ограничен с
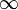 до числа цифр в числе - n-1. Частные суммы являются суммами k-тых степеней числа Эйлера е=2,71... без членов, в которых ak=0.
до числа цифр в числе - n-1. Частные суммы являются суммами k-тых степеней числа Эйлера е=2,71... без членов, в которых ak=0.при аk из a={0,1,2} и b=е=2,71… образуется (3,e)-ричная система счисления
(3,e)-ричная система счисления хорошо подходит для вычислений в (3,е)-ричной системе счисления на троичных эвм,
при ak из a={0,1,2,3,4,5,6,7,8,9} и b=e=2,71… образуется (10,e)-ричная система счисления
(10,е)-ричная система хорошо подходит для вычислений в (10,е)-ричной системе счисления на эвм имеющих десятичную арифметику.
Перевод десятичных чисел в (2,е)-ричные числа
Перевод кратных е десятичных чисел ((2,e)-целых) в (2,e)-ричные числа ((2,e)-целые). 2,71...10,10=е10,10=12,e
5,44...10,10=2e10,10=102,e
8,15...10,10=3e10,10=112,e
...
27,1...10,10=10e10,10=10102,e
...
271,...10,10=100e10,10=11001002,e
...Перевод (2,е)-ричных чисел в десятичные числа
Перевод (2,e)-целых чисел ((2,e)-целых) в десятичные дробные числа кратные e.
12,e=e10,10=2,71...10,10
102,e=2e10,10=5,44...10,10
112,e=3e10,10=8,15...10,10
...
10102,e=10e10,10=27,1...10,10
...
11001002,e=100e10,10=271,...10,10
...
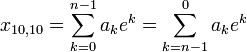
Перевод дробных (2,e)-чисел в десятичные дробные числа.
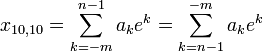
Перевод двоичных чисел в (2,е)-ричные числа
Перевод (2,е)-ричных чисел в двоичные числа
Перевод троичных чисел в (2,е)-ричные числа
Перевод (2,е)-ричных чисел в троичные числа
Сдвоенные позиционные показательные троичные системы счисления
при ak из a={0,1,2} и b=3 образуется (3,3)-ичная (обычная) троичная система счисления
Сдвоенные позиционные показательные десятичные системы счисления
при ak из a={0,1,2,3,4,5,6,7,8,9} и b=10 образуется (10,10)-ичная (обычная) десятичная система счисления
Стро́енные показательные системы счисления
Частным случаем комбинированных систем счисления являются строенные показательные позиционные системы счисления с дополнительными весовыми коэффициентами разрядов, в которых используются три системы счисления:
- внутриразрядная система с числами ak, цифры которой используются для кодирования цифр внутри разрядов,
- межразрядная система счисления с основанием b и
- дополнительная система счисления с основанием c, например, в дополнительном сомножителе (b/c) в весовом коэффициенте разряда,
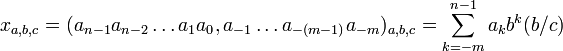 , где:
, где:
- n — число разрядов целой части числа,
- m — число разрядов дробной части числа.
- k — номер разряда,
- a — основание основной внутриразрядной системы счисления,
- ak — цифры внутриразрядной системы счисления в числовых разрядах,
- b — основание межразрядной системы счисления,
- c — основание дополнительной системы счисления, в общем случае c≠b, при целом c образуются комбинированные (a, b,c)-ричные системы счисления, при c=b образуются обычные (a, b)-ричные позиционные системы счисления,
Стро́енные позиционные показательные e-ричные системы счисления
Числа x, кратные e/c, в (a,e,c)-ричных показательных позиционных системах счисления представляются в виде конечной линейной комбинации произведений степеней числа e («е/c-целые») на дополнительные весовые коэффициенты (е/с):
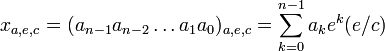 , где:
, где:
ek — основной весовой коэффициент разрядов,
c — основание вспомогательной системы счисления, число цифр используемых для записи одного (a,е,c)-ричного разряда,
(e/c) — дополнительный весовой коэффициент разрядов,
ak — (a,e,c)-ричные цифры, которые
в (a,е,2)-ричной системе счисления могут принимать только два значения: 0 или 1 с весами цифр 0*е/2 и 1*е/2;
в (a,e,3)-ричной системе счисления могут принимать три значения: 0, 1 и 2 с весами цифр 0*е/3, 1*e/3 и 2*е/3;
в (a,e,10)-ричной системе счисления могут принимать десять значений: от 0 до 9 с весами цифр 0*е/10, 1*e/10, 2*e/10, 3*e/10, 4*e/10, 5*e/10, 6*e/10, 7*e/10, 8*e/10 и 9*e/10.
Числа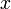 , некратные e/c, представляются в виде «е/c-дробных» чисел:
, некратные e/c, представляются в виде «е/c-дробных» чисел: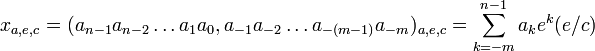 , где:
, где:
m — число знаков «е/с-дробной» части числа (справа от запятой).
(a,е,2)-ричная система счисления хорошо подходит для вычислений в е-ричной системе счисления на двоичных ЭВМ.
(a,e,3)-ричная система счисления хорошо подходит для вычислений в е-ричной системе счисления на троичных ЭВМ.
(a,е,10)-ричная система хорошо подходит для вычислений в е-ричной системе счисления на ЭВМ имеющих десятичную арифметику.
Как можно заметить, в (a,е,c)-ричных системах счисления для записи чисел в разрядах возможны цифры неравные межразрядному основанию системы счисления — е.См. также
- Системы счисления
- Позиционные системы счисления
- Двоичная система счисления
- Троичные системы счисления
- Десятичная система счисления
- Е-ричная система счисления
Ссылки
- ↑ 1 2 Популярные лекции по матеметике. Выпуск 40. С. В. Фомин. Системы счисления. Издание пятое. Москва, «Наука», Главная редакция физико-математической литературы, 1987
- ↑ http://eqworld.ipmnet.ru/ru/library/mathematics/handbooks.htm Выгодский М.Я. Справочник по высшей математике (12-е изд.). М.: Наука, 1977 (djvu)
- С. В. Фомин Системы счисления. — М.: Наука, 1987. — 48 с. — (Популярные лекции по математике). (§ 14. Об одном замечательном свойстве троичной системы. Стр.39-40, Рис.4)
Wikimedia Foundation. 2010.

![x_{a} = (a_{n-1} a_{n-2}\dots a_{1} a_{0},a_{-1} a_{-2}\dots a_{-(m-1)} a_{-m})_{a}=\Bigl[ F(f(a_k)) \Bigr]_{k=-m}^{n-1}](http://dic.academic.ru/pictures/wiki/files/53/558c2b6649fd9ced4d0b790d0db37410.png)