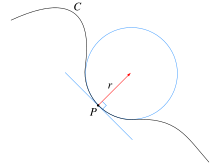
Соприкасающаяся окружность

Соприкаса́ющаяся окру́жность, окру́жность кривизны́ — окружность, являющаяся наилучшим приближением заданной кривой в окрестности данной точки. В этой точке кривая и означенная окружность испытывают касание, порядок которого не ниже 2. Окружность кривизны существует в каждой точке дважды дифференцируемой кривой с отличной от нуля кривизной; в случае нулевой кривизны в качестве соприкасающейся надлежит рассматривать касательную прямую — «окружность бесконечного радиуса».

Соприкасающаяся окружность (или прямая) в точке $P$ кривой также может быть определена как предельное положение окружности (или прямой), проходящей через $P$ и две близкие к ней точки $P_1,\ P_2$, когда $P_1,\ P_2$ стремятся к $P$.

Связанные определения

Центр соприкасающейся окружности называют центром кривизны, а радиус — радиусом кривизны. Радиус кривизны является величиной, обратной кривизне кривой в заданной точке:

$R^{-1} = k$

Центр соприкасающейся окружности всегда лежит на главной нормали кривой; отсюда следует, что эта нормаль всегда направлена в сторону вогнутости кривой.

Геометрическое место центров кривизны кривой называется эволютой.

Свойства

• Теорема Кнесера. Если кривизна плоской кривой строго монотонна, то её соприкасающиеся окружности не пересекаются друг с другом.

История

Понятие соприкасающейся окружности (лат. circulum osculans) было введено Лейбницем.