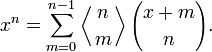- Эйлера числа
-
В комбинаторике числом Эйлера I рода из n по k, обозначаемым
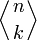 или E(n,k), называется количество перестановок порядка n с k подъёмами, то есть таких перестановок
или E(n,k), называется количество перестановок порядка n с k подъёмами, то есть таких перестановок 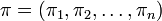 , что существует ровно k индексов j, для которых πj < πj + 1.
, что существует ровно k индексов j, для которых πj < πj + 1.Числа Эйлера I рода обладают также геометрической и вероятностной интерпретацией: число
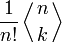 выражает n-мерный объём части n-мерного гиперкуба, ограниченного (n − 1)-мерными гиперплоскостями
выражает n-мерный объём части n-мерного гиперкуба, ограниченного (n − 1)-мерными гиперплоскостями 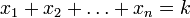 и
и 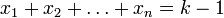 ; оно же выражает вероятность того, что сумма n независимых переменных с равномерным распределением в отрезке [0,1] лежит между k − 1 и k.
; оно же выражает вероятность того, что сумма n независимых переменных с равномерным распределением в отрезке [0,1] лежит между k − 1 и k.Содержание
Пример
Перестановки π четвертого порядка, имеющие ровно два подъёма, должны удовлетворять одному из двух неравенств: π1 < π2 < π3 > π4 или π1 > π2 < π3 < π4. Таких перестановок ровно 11 штук:
- 1324 1423 2314 2413 3412 1243 1342 2341 2134 3124 4123
Поэтому
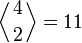 .
.Свойства
Для заданного натурального числа n существует единственная перестановка без подъёмов, то есть
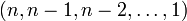 . Также существует единственная перестановка, которая имеет n − 1 подъёмов, то есть
. Также существует единственная перестановка, которая имеет n − 1 подъёмов, то есть 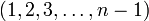 . Таким образом,
. Таким образом,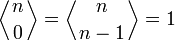 для всех натуральных n.
для всех натуральных n.
Зеркальным отражением перестановки с m подъёмами является перестановка с n − m − 1 подъёмами. Таким образом,
Треугольник чисел Эйлера первого рода
Значение чисел Эйлера
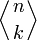 для малых значений n и k приведены в следующей таблице (последовательность A008292 в OEIS):
для малых значений n и k приведены в следующей таблице (последовательность A008292 в OEIS):n/k 0 1 2 3 4 5 6 7 8 9 0 1 1 1 0 2 1 1 0 3 1 4 1 0 4 1 11 11 1 0 5 1 26 66 26 1 0 6 1 57 302 302 57 1 0 7 1 120 1191 2416 1191 120 1 0 8 1 247 4293 15619 15619 4293 247 1 0 9 1 502 14608 88234 156190 88234 14608 502 1 0 Легко понять, что значения на главной диагонали матрицы задаются формулой:
![\left\langle{n\atop n}\right\rangle=[n=0].](/pictures/wiki/files/102/f44fd815c782fd05d098b9ce9d54a7ca.png)
Треугольник Эйлера, как и треугольник Паскаля, симметричен слева и справа. Но в этом случае закон симметрии несколько отличен:
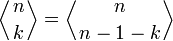 при n > 0. То есть перестановка имеет n − 1 − k подъёмов тогда и только тогда, когда её «отражение» имеет k подъёмов.
при n > 0. То есть перестановка имеет n − 1 − k подъёмов тогда и только тогда, когда её «отражение» имеет k подъёмов.Рекуррентная формула
Каждая перестановка
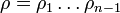 из набора {1,2,3,n − 1} приводит к n перестановкам из {1,2,3,n}, если мы вставляем новый элемент n всеми возможными способами. Вставляя n в j-ю позицию, получаем перестановку
из набора {1,2,3,n − 1} приводит к n перестановкам из {1,2,3,n}, если мы вставляем новый элемент n всеми возможными способами. Вставляя n в j-ю позицию, получаем перестановку 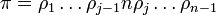 . Количество подъёмов в ρ равняется количеству подъёмов в ρ, если j = 1 или если πj − 1 < πj; и оно больше количества подъёмов в ρ, если j = n или если ρj − 1 > ρj. Следовательно, π в сумме имеет
. Количество подъёмов в ρ равняется количеству подъёмов в ρ, если j = 1 или если πj − 1 < πj; и оно больше количества подъёмов в ρ, если j = n или если ρj − 1 > ρj. Следовательно, π в сумме имеет 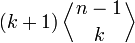 способов построения перестановок из ρ, которые имеют k подъёмов, плюс
способов построения перестановок из ρ, которые имеют k подъёмов, плюс 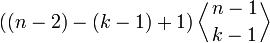 способов построения перестановок из ρ, которые имеют k − 1 подъёмов. Тогда искомая рекуррентная формула для целых n > 0 имеет вид:
способов построения перестановок из ρ, которые имеют k − 1 подъёмов. Тогда искомая рекуррентная формула для целых n > 0 имеет вид:Положим также, что
![\left\langle{0\atop k}\right\rangle = [k=0]](/pictures/wiki/files/49/184ed9768b13c25d6924187b67d58fbc.png) (для целых k), и предположим, что при k < 0.
(для целых k), и предположим, что при k < 0.Связь с биномиальными коэффициентами и степенными функциями
Применение чисел Эйлера главным образом состоит в предоставлении замечательной связи между обычными степенями и последовательными биномиальными коэффициентами:
для целых
 . (Это тождество также известно под названием тождества Верпинского). В частности:
. (Это тождество также известно под названием тождества Верпинского). В частности:и т. д. Эти тождества легко доказываются по индукции.
В этой связи нужно отметить, что эта формула предоставляет ещё один способ вычисления суммы первых n квадратов:
Явные формулы для чисел Эйлера
Поскольку рекуррентность для чисел Эйлера достаточно сложная, они удовлетворяют лишь немногим свойствам:
Умножая первое тождество на zn − m и суммируя по m, получаем:
Заменяя z на z + 1 и уравнивая коэффициенты при zk, получаем второе тождество. Таким образом, эти два тождества эквивалентны. Первое тождество применяется при малых значениях m:
Суммирование чисел Эйлера I рода
Из комбинаторного определения очевидно, что сумма чисел Эйлера I рода, расположенных в n-й строке равна n!, так как она равна количеству всех перестановок порядка n:
Знакопеременные суммы чисел Эйлера I рода при фиксированном значении n связаны с числами Бернулли Bn + 1:
Также справедливы следующие тождества:
Производящая функция и тождество Ворпицкого
Производящая функция чисел Эйлера I рода имеет вид:
Числа Эйлера I рода связаны также с производящей функцией последовательности n-х степеней:
Кроме того, Z-преобразование из
является генератором первых N строк треугольник чисел Эйлера, когда знаменатель n-й элемента преобразования сокращается умножением на (z − 1)j + 1:
Тождество Ворпицкого выражает xn как сумму обобщенных биномиальных коэффициентов:
Программы на PARI/GP для вычисления чисел Эйлера
\\ рекуррентная формула { E(n, k) = if(k<1|k>n, 0, if(n==1, 1, k*E(n-1,k) + (n-k+1)*E(n-1,k-1) ) ) } \\ явная формула { E(n, k) = sum(j=0, k, (-1)^j * (k-j)^n * binomial(n+1,j) ) }Литература
- Дональд Кнут, Роналд Грэхем, Орен Паташник Числа Эйлера // Конкретная математика. Основание информатики = Concrete Mathematics. A Foundation for Computer Science. — М.: Мир; Бином. Лаборатория знаний, 2006. — С. 703. — ISBN 5-94774-560-7
- Д. Кнут. Искусство программирования. Т.1: Основные алгоритмы — М.: Вильямс — 2006 г.
- Eric W. Weisstein, Eulerian Number at MathWorld
- Eric W. Weisstein, Worpitzky’s Identity at MathWorld
- Eulerian Numbers at MathPages
Wikimedia Foundation. 2010.

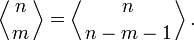
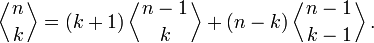
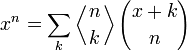
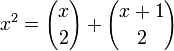
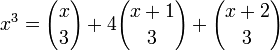
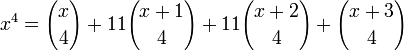
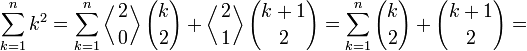
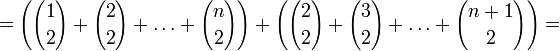
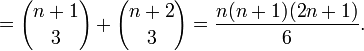
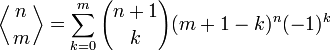
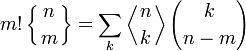
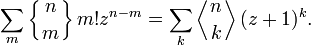
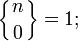
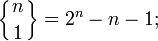
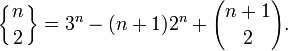
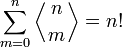
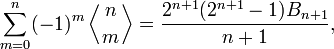
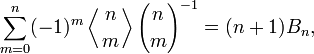
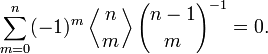
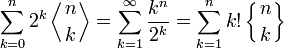
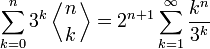
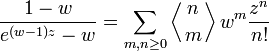
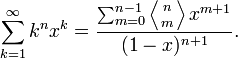
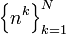
![Z\left [ \{n^k\}_{k=1}^3 = \left\{ \frac{z}{(z-1)^2}, \frac{z+z^2}{(z-1)^3}, \frac{z+4z^2+z^3}{(z-1)^4} \right\}\right]](/pictures/wiki/files/102/f617150d2a40ffaf7981ba18e476e404.png)