Числа Скьюза

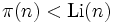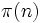Число Скьюза (англ. Skewes number) — наименьшее целое число n такое, что $\pi(n)<\mathrm{Li}(n)\,\!$, где $\pi(n)\,\!$ — количество простых чисел, не превосходящих 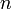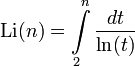$n\,\!$, $\mathrm{Li}(n)=\int\limits_2^n \frac{dt}{\ln(t)}$ — сдвинутый интегральный логарифм.

Джон Литтлвуд в 1914 дал неконструктивное доказательство того, что такое число существует.

Стенли Скьюз в 1933 оценил это число, исходя из гипотезы Римана, как 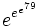$e^{e^{e^{79}}}\,\!$ — первое число Скьюза, обозначается Sk₁.

В 1955 он же дал оценку без предположения о верности гипотезы Римана: 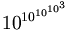$10^{10^{10^{10^3}}}$ — второе число Скьюза, обозначается Sk₂. Это одно из самых больших чисел, когда-либо применявшихся в математических доказательствах.

В 1987 Риел (H. J. J. te Riele) без предположения гипотезы Римана свёл число Скьюза к 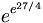$e^{e^{27/4}}$, что приблизительно равно 8,185·10³⁷⁰.