- Центральная предельная теорема для мартингалов
-
Центра́льные преде́льные теоре́мы (Ц.П.Т.) — класс теорем в теории вероятностей, утверждающих, что сумма большого количества независимых случайных величин имеет распределение, близкое к нормальному. Так как многие случайные величины в приложениях являются суммами нескольких случайных факторов, центральные предельные теоремы обосновывают популярность нормального распределения.
Содержание
Классическая формулировка Ц.П.Т.
Пусть
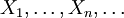 есть бесконечная последовательность независимых одинаково распределённых случайных величин, имеющих конечное математическое ожидание и дисперсию. Обозначим последние μ и σ2, соответственно. Пусть
есть бесконечная последовательность независимых одинаково распределённых случайных величин, имеющих конечное математическое ожидание и дисперсию. Обозначим последние μ и σ2, соответственно. Пусть 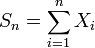 . Тогда
. Тогда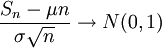 по распределению при
по распределению при 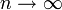 ,
,
где N(0,1) — нормальное распределение с нулевым математическим ожиданием и стандартным отклонением, равным единице. Обозначив символом
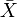 выборочное среднее первых n величин, то есть
выборочное среднее первых n величин, то есть 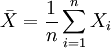 , мы можем переписать результат центральной предельной теоремы в следующем виде:
, мы можем переписать результат центральной предельной теоремы в следующем виде: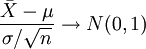 по распределению при
по распределению при 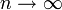 .
.
Замечания
- Неформально говоря, классическая центральная предельная теорема утверждает, что сумма n независимых одинаково распределённых случайных величин имеет распределение, близкое к N(nμ,nσ2). Эквивалентно,
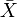 имеет распределение близкое к N(μ,σ2 / n).
имеет распределение близкое к N(μ,σ2 / n). - Так как функция распределения стандартного нормального распределения непрерывна, сходимость к этому распределению эквивалентна поточечной сходимости функций распределения к функции распределения стандартного нормального распределения. Положив
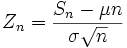 , получаем
, получаем 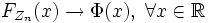 , где Φ(x) — функция распределения стандартного нормального распределения.
, где Φ(x) — функция распределения стандартного нормального распределения. - Центральная предельная теорема в классической формулировке доказывается методом характеристических функций (теорема Леви о непрерывности).
- Вообще говоря, из сходимости функций распределения не вытекает сходимость плотностей. Тем не менее в данном классическом случае имеет место
Локальная Ц.П.Т.
В предположениях классической формулировки, допустим в дополнение, что распределение случайных величин
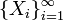 абсолютно непрерывно, то есть оно имеет плотность. Тогда распределение Zn также абсолютно непрерывно, и более того,
абсолютно непрерывно, то есть оно имеет плотность. Тогда распределение Zn также абсолютно непрерывно, и более того,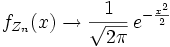 при
при 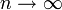 ,
,
где
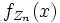 - плотность случайной величины Zn, а в правой части стоит плотность стандартного нормального распределения.
- плотность случайной величины Zn, а в правой части стоит плотность стандартного нормального распределения.Некоторые обобщения
Результат классической центральной предельной теоремы справедлив для ситуаций гораздо более общих, чем полная независимость и одинаковая распределённость.
Ц.П.Т. Линдеберга
Пусть независимые случайные величины
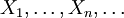 определены на одном и том же вероятностном пространстве и имеют конечные математические ожидания и дисперсии:
определены на одном и том же вероятностном пространстве и имеют конечные математические ожидания и дисперсии: ![\mathbb{E}[X_i] = \mu_i,\; \mathrm{D}[X_i] = \sigma^2_i](/pictures/wiki/files/100/d3facc3352c1441bdc91fcc54a084cf9.png) . Как и прежде построим частичные суммы
. Как и прежде построим частичные суммы 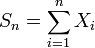 . Тогда в частности,
. Тогда в частности, ![\mathbb{E}[S_n] = m_n = \sum\limits_{i=1}^n \mu_i,\; \mathrm{D}[S_n] = s_n^2 = \sum\limits_{i=1}^n \sigma_i^2](/pictures/wiki/files/51/3c98026e8c0032db0ca43a43a7421d9c.png) . Наконец, пусть выполняется условие Линдеберга:
. Наконец, пусть выполняется условие Линдеберга:Тогда
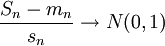 по распределению при
по распределению при 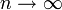 .
.
Ц.П.Т. Ляпунова
Пусть выполнены базовые предположения Ц.П.Т. Линдеберга. Пусть случайные величины {Xi} имеют конечный третий момент. Тогда определена последовательность
![r^3_n = \sum_{i=1}^n \mathbb{E}\left[|X_i-\mu_i|^3\right]](/pictures/wiki/files/55/73c7058fa9e796e84b8538a5382bbd68.png) . Если предел
. Если предел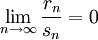 (условие Ляпунова),
(условие Ляпунова),
то
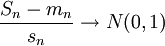 по распределению при
по распределению при 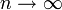 .
.
Ц.П.Т. для мартингалов
Пусть процесс
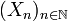 является мартингалом. Введём случайные процессы
является мартингалом. Введём случайные процессы 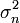 и τn следующим образом:
и τn следующим образом:и
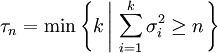 .
.
Тогда
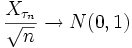 по распределению при
по распределению при 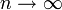 .
.
Wikimedia Foundation. 2010.

![\forall \varepsilon>0,\; \lim\limits_{n\to \infty}\sum\limits_{i=1}^n \mathbb{E}\left[\frac{(X_i-\mu_i)^2}{s_n^2}\, \mathbf{1}_{\{|X_i-\mu_i|> \varepsilon s_n\}}\right] = 0.](/pictures/wiki/files/99/c0fd6915307b0fbc5064a26eace04be6.png)
![\sigma_n^2 = \mathbb{E} \left[(X_{n+1}-X_n)^2 \mid X_1 ,\ldots, X_n\right]](/pictures/wiki/files/53/53252f5788cf0fb367a1da7bcf5de5d0.png)