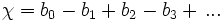Характеристика Эйлера

В алгебраической топологии, эйлерова характеристика есть топологический инвариант (и даже гомотопический инвариант) определённый на большом классе топологических пространств. Обычно эйлерова характеристика пространства X обозначается χ(X).

Эйлерова характеристика двумерных топологических полиэдров может быть посчитана по формуле: χ = Γ - P + B где Г, Р и В суть числа граней, рёбер и вершин соответственно. В частности, для любого выпуклого многогранника верна формула Эйлера:

Γ - P + B = χ(S²) = 2.

Например, для куба 6 − 12 + 8 = 2 и для треугольной пирамиды 4 − 6 + 4 = 2.

Определения и свойства

• Для конечного клеточного комплекса (в частности для конечного симплициального комплекса) эйлерова характеристика может быть определена как знакопеременная сумма

  χ = k₀ - k₁ + k₂ - ...,

где k_i обозначает число клеток размерности i.

• Эйлерова характеристика произвольного топологического пространства может быть определена через числа Бетти b_n как знакопеременная сумма:

  $\chi=b_0 - b_1 + b_2 - b_3 +\, ...$

Это определение имеет смысл только если все числа Бетти конечны и обнуляются для всех достаточно больших индексов.

• Последнее определение обобщает предыдущее и обобщается на другие гомологии с произвольными коэффициентами.

• Например окружность и тор имеют характеристику 0, а шар имеет характеристику 1.
• Эйлерова характеристика сферы с g ручками равна

  2 - 2g.

• Согласно формуле Гаусса — Бонне, эйлерова характеристика замкнутой поверхности S равна

  $\chi(S)=\int\limits_SK$

где K обозначает гауссову кривизну.

• Обобщённая формула Гаусса — Бонне даёт похожую формулу для произвольных замкнутых римановых многообразий.
• Существует также дискретный аналог теоремы Гаусса — Боне, гласящий, что эйлерова характеристика равна сумме дефектов полиэдра делённой на 2π.

• Если два пространства гомотопически эквивалентны то их числа Бетти совпадают, а таким образом и эйлеровы характеристики совпадают.

Литература

• Долбилин Н., Три теоремы о выпуклых многогранниках, Квант, № 5, 2001.
• Лакатос И. Доказательства и опровержения. Как доказываются теоремы. Пер. И. Н. Веселовского. М.: Наука, 1967.
• Шашкин Ю. А. Эйлерова характеристика. Популярные лекции по математике, Выпуск 58, М., «Наука» 1984 г.

См. также

• Список объектов, названных в честь Леонарда Эйлера