ЭЙЛЕРОВА ХАРАКТЕРИСТИКА

конечного клеточного комплекса К - целое число

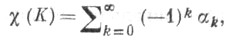
где - число k-мерных клеток комплекса. Названа в честь Л. Эйлера (L. Enler), к-рый доказал в 1758, что число вершин В, ребер Р и граней Г. выпуклого многогранника связаны формулой В-Р+Г=2. В неявном виде эта формула была известна еще Р. Декарту (R. Descarles, 1620). Оказывается, что

где p^k есть k-мерное Бетти число комплекса К(формула Эйлера - Пуанкаре). Э. х. комплекса Кявляется его гомологическим, гомотопическим и топологическим инвариантом. В частности, Э. х. не зависит от способа разбиения пространства на клетки. Поэтому можно говорить, напр., об Э. х. произвольного компактного полиэдра, понимая под этим Э. <х. какой-нибудь его триангуляции. С другой стороны, формула Эйлера-Пуанкаре позволяет распространить понятие Э. х. на более широкий класс пространств и пар пространств, для к-рых правая часть формулы имеет смысл. Для произвольного поля Fсправедлива обобщенная формула Эйлера - Пуанкаре, выражающая Э. х. через
размерности над полем F групп гомологии с коэффициентами в поле F:

Пусть - локально тривиальное расслоение со слоем F. Тогда, при нек-рых ограничениях на пространства К, В, F, их Э. х. связаны соотношением В частности, Э. х. прямого произведения двух пространств равна произведению их Э. х. С помощью соотношения 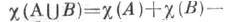справедливого для любой вырезаемой триады вычисляются Э. х. всех компактных двумерных многообразий. Э. х. сферы с . ручками и kудаленными открытыми дисками равна 2-2g-k, сферы с то листами Мёбиуса и kудаленными дисками - 2- т-k. Э. х. произвольного компактного многообразия нечетной размерности равна половине Э. х. его края. В частности, Э. х. замкнутого многообразия нечетной размерности равна нулю, так как его край пуст.

С. В. Матвеев.