Функция, аналитическая

Определение

Аналитическая функция (действительного переменного) — функция, которая совпадает со своим рядом Тейлора в окрестности любой точки области определения.

Однозначная функция f называется аналитической в точке z₀, если сужение функции f на некоторую окрестность z₀ является аналитической функцией. Если функция аналитична в точке z₀, то она аналитическая в каждой точке некоторой окрестности точки z₀.

Аналитическая функция (комплексного переменного) — функция комплексного переменного f(z) = u(z) + iv(z) (где u(z) и v(z) — вещественнозначные функции комплексного переменного, являющиеся, соответственно, вещественной и мнимой частью рассматриваемой функции), для которой в некоторой области 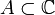$A\subset\mathbb C$, называемой областью аналитичности, выполняется одно из трех равносильных условий:

1. Для вещественной и мнимой части этой функции в каждой точке $z=x+iy\in A$ выполняются условия Коши — Римана (аналитичность в смысле Коши — Римана);
2. Ряд Тейлора функции в каждой точке $z\in A$ сходится и его сумма равна f(z) (аналитичность в смысле Вейерштрасса);
3. Интеграл $\int\limits_\Gamma\,f(z)\,dz=0$ для любой замкнутой кривой $\Gamma\subset A$ (аналитичность в смысле Коши)

В курсе комплексного анализа доказывается эквивалентность трех определений.

Свойства

1. Если f(z) и g(z) аналитичны в области 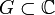$G\subset\mathbb C$, то аналитическими в G также будут функции 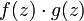$f(z)\pm g(z)$, $f(z)\cdot g(z)$ и $f(g(z))\,$.
2. Если g(z) в области G не обращается в ноль, то $\frac{f(z)}{g(z)}$ будет аналитична в G
3. Если f'(z) в области G не обращается в ноль, то f ^{− 1}(z) будет аналитична в G.

Некоторые свойства аналитических функций близки к свойствам многочленов, что, впрочем, и неудивительно — определение аналитичности в смысле Вейерштрасса свидетельствует о том, что аналитические функции — в некотором роде предельные варианты многочленов. Допустим, согласно основной теореме алгебры любой многочлен может иметь нулей числом не более его степени. Для аналитических функций справедливо аналогичное утверждение, вытекающее из теоремы единственности в альтернативной форме — множество нулей аналитической в односвязной области функции не может иметь в этой области предельных точек, в противном случае функция тождественно равна нулю.

Примеры

Все многочлены являются аналитическими функциями во всей плоскости 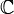$\mathbb C$. Далее, аналитическими (правда, в большинстве случаев в каких-то определенных областях) являются элементарные функции.

Но:

1. Функция f(z) = | z | не является аналитической в 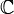$\mathbb C$, так как она не имеет прозводной в точке z = 0.
2. Функция $f(z)=\overline{z}$ не является аналитической по тем же соображениям. Однако её сужение на вещественную ось будет аналитической функцией, так как оно будет совпадать с сужением функции f(z) = z.