- АНАЛИТИЧЕСКАЯ КРИВАЯ
аналитическая дуга,- кривая K n-мерного евклидова пространства
 допускающая аналитич. араметризацию. Это означает, что координаты ее точек
допускающая аналитич. араметризацию. Это означает, что координаты ее точек 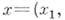
 могут быть выражены в виде аналитич. функций действительного параметра
могут быть выражены в виде аналитич. функций действительного параметра 
 т. е. в нек-рой окрестности каждой точки t0,
т. е. в нек-рой окрестности каждой точки t0, 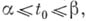 функции
функции 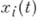 представимы в виде сумм сходящихся степенных рядов по степеням
представимы в виде сумм сходящихся степенных рядов по степеням  причем производные
причем производные 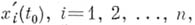 не равны нулю одновременно ни в одной точке отрезка
не равны нулю одновременно ни в одной точке отрезка 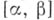 . Последнее условие иногда оговаривают дополнительно, называя удовлетворяющую ему А. к. правильной. А. к. наз. замкнутой, если
. Последнее условие иногда оговаривают дополнительно, называя удовлетворяющую ему А. к. правильной. А. к. наз. замкнутой, если 
На плоскости
 комплексного переменного
комплексного переменного  =
= А. к. допускает представление в виде комплексной аналитич. функции действительного параметра
А. к. допускает представление в виде комплексной аналитич. функции действительного параметра  Если А. к. расположена в области
Если А. к. расположена в области  то при конформном отображении
то при конформном отображении  на к.-л. область она отображается также в А. к.
на к.-л. область она отображается также в А. к.
Если множество точек пересечения двух А. к. бесконечно, то эти А. к. совпадают.
Вообще, в комплексном пространстве
 комплексные координаты
комплексные координаты  точек А. к. допускают представление в виде аналитич. функций действительного параметра
точек А. к. допускают представление в виде аналитич. функций действительного параметра  Следует, однако, иметь в виду, что при
Следует, однако, иметь в виду, что при 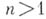 термин "А. к." иногда обозначает аналитическую поверхность комплексной размерности единица.
термин "А. к." иногда обозначает аналитическую поверхность комплексной размерности единица.
На рцмановой поверхности SА. к. Кдопускает представление вида
 - локальный униформизирующий параметр точек Рповерхности S,
- локальный униформизирующий параметр точек Рповерхности S, 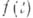 -аналитич. функция действительного параметра в окрестности любой точки
-аналитич. функция действительного параметра в окрестности любой точки 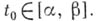
Лит.:[1] Маркушевич А. И., Теория аналитических функций, т. 2, М., 1968; гл. 8; [2] Шабат Б. В., Введение в комплексный анализ, ч. 1-2, 2изд., М., 1976.
Е. Д. Соломенцев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
