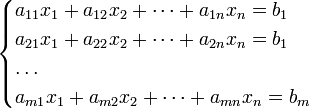СЛАУ

Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида

$\begin{cases} a_{11}x_1 + a_{12}x_2 + \dots + a_{1n}x_n = b_1 \\ a_{21}x_1 + a_{22}x_2 + \dots + a_{2n}x_n = b_1\\ \dots\\ a_{m1}x_1 + a_{m2}x_2 + \dots + a_{mn}x_n = b_m \\ \end{cases}$

(1)

Здесь x₁, x₂, …, x_n — неизвестные, которые надо определить. a₁₁, a₁₂, …, a_mn — коэффициенты системы — и b₁, b₂, … b_m — свободные члены — предполагаются известными. Индексы коэффициентов (a_ij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно^[1].

Система (1) называется однородной, если все её свободные члены равны нулю (b₁ = b₂ = … = b_m = 0), иначе — неоднородной.

Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.

Решение системы (1) — совокупность n чисел c₁, c₂, …, c_n, таких что подстановка каждого c_i вместо x_i в систему (1) обращает все ее уравнения в тождества.

Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения.

Совместная система вида (1) может иметь одно или более решений.

Решения c₁⁽¹⁾, c₂⁽¹⁾, …, c_n⁽¹⁾ и c₁⁽²⁾, c₂⁽²⁾, …, c_n⁽²⁾ совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:

c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).

Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у нее есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.

Матричная форма

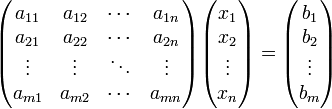
Система линейных уравнений может быть представлена в матричной форме как:

$\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} = \begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_m \end{pmatrix}$

или, согласно правилу перемножения матриц,

AX = B.

Если к матрице А прибавить столбец свободных членов, то А называется расширенной матрицей.

Методы решения

Прямые (или точные) методы, позволяют найти решение за определенное количество шагов. Итерационные методы, основаны на использовании повторяющегося процесса и позволяют получить решение в результате последовательных приближений

Прямые методы

• Метод Гаусса
• Метод Гаусса — Жордана
• Метод Крамера
• Матричный метод
• Метод прогонки (для трёхдиагональных матриц)
• Разложение Холецкого или метод квадратных корней (для положительно-определённых симметричных и эрмитовых матриц)

Итерационные методы

• Метод Якоби (метод простой итерации)
• Метод Гаусса — Зейделя
• Метод релаксации
• Многосеточный метод

Решение системы линейных алгебраических уравнений на VBA

  Option Explicit
 
 
    Sub rewenie()
 
    Dim i As Integer
    Dim j As Integer
    Dim r() As Double
    Dim p As Double
    Dim x() As Double
    Dim k As Integer
    Dim n As Integer
    Dim b() As Double
    Dim file As Integer
    Dim y() As Double
 
    file = FreeFile
    Open "C:\data.txt" For Input As file
    Input #file, n
    ReDim x(0 To n * n - 1) As Double
    ReDim y(0 To n - 1) As Double
    ReDim r(0 To n - 1) As Double
 
    For i = 0 To n - 1
        For j = 0 To n - 1
            Input #file, x(i * n + j)
        Next j
        Input #file, y(i)
    Next i
 
    Close #file
 
 
    For i = 0 To n - 1
    p = x(i * n + i)
        For j = 1 To n - 1
            x(i * n + j) = x(i * n + j) / p
        Next j
        y(i) = y(i) / p
            For j = i + 1 To n - 1
            p = x(j * n + i)
                For k = i To n - 1
                    x(j * n + k) = x(j * n + k) - x(i * n + k) * p
                Next k
            y(j) = y(j) - y(i) * p
        Next j
Next i
' Верхнетреугольная матрица
 
For i = n - 1 To 0 Step -1
p = y(i)
    For j = i + 1 To n - 1
    p = p - x(i * n + j) * r(j)
    Next j
r(i) = p / x(i * n + i)
Next i
 
' Обратный ход
For i = 0 To n - 1
MsgBox r(i)
Next i
 
 
'<!--End of Code-->
 
 
End Sub

См. также

• Недоопределённая система
• Теорема Кронекера — Капелли
• Решение систем линейных алгебраических уравнений

Ссылки

• Решение СЛАУ онлайн

Примечания

1. ↑ Ильин В. А., Позняк Э. Г. Линейная алгебра: Учебник для вузов. — 6-е изд., стер. — М.: ФИЗМАТЛИТ, 2004. — 280 с.