Оригинал (операционное исчисление)
- Оригинал (операционное исчисление)
-
Функция-оригинал — фундаментальное понятие в операционном исчислении; для того, чтобы функция  могла называться оригиналом, она должна удовлетворять трем условиям:
могла называться оригиналом, она должна удовлетворять трем условиям:
- f удовлетворяет условию Гёльдера почти всюду на вещественной прямой
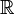 , притом на произвольном конечном интервале
, притом на произвольном конечном интервале  множество точек, в которых указанное условие не выполняется, конечно, притом в этих точках она должна претерпевать разрыв 1-го рода. Формально, для произвольного t, не относящегося к упомянутому множеству, должны существовать положительные постоянные
множество точек, в которых указанное условие не выполняется, конечно, притом в этих точках она должна претерпевать разрыв 1-го рода. Формально, для произвольного t, не относящегося к упомянутому множеству, должны существовать положительные постоянные  , такие, что
, такие, что  для произвольного
для произвольного ![h\in[-h_0;h_0]](/pictures/wiki/files/102/f13821f8f6d6aef162645b7aa925d203.png) .
.
- f(t) = 0 при t < 0.
- на функцию f(t) накладывается определённое ограничение — она должна возрастать не быстрее показательной функции. Формально, для этой функции должны существовать постоянные
 такие, что
такие, что  для произвольного
для произвольного  .
.
Для большинства физических задач все эти три условия соблюдены. Более того, с использованием функции Хевисайда H(t) можно получить функцию-оригинал из функции, удовлетворяющей только условиям 1 и 3.
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Оригинал (операционное исчисление)" в других словарях:
Операционное исчисление — один из методов математического анализа, позволяющий в ряде случаев с помощью весьма простых средств решать сложные математические задачи. Содержание 1 История 2 Свойства изображений … Википедия
Операционное исчисление — один из методов математического анализа, позволяющий в ряде случаев посредством простых правил решать сложные математические задачи. О. и. имеет особенно важное значение в механике, автоматике, электротехнике и др. В основе метода О. и.… … Большая советская энциклопедия
Функция-оригинал — фундаментальное понятие в операционном исчислении; для того, чтобы функция могла называться оригиналом, она должна удовлетворять трем условиям: удовлетворяет условию Гёльдера почти всюду на вещественной прямой , притом на произвольном конечном… … Википедия
Преобразование Лапласа — Преобразование Лапласа интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются… … Википедия
Лапласа преобразование — Преобразование Лапласа интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и … Википедия
Обратное преобразование Лапласа — Преобразование Лапласа интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и … Википедия
ЛАПЛАСА ПРЕОБРАЗОВАНИЕ — трансформация Лапласа, в широком смысле интеграл Лапласа вида где интегрирование производится по нек рому контуру Lв плоскости комплексного переменного z, ставящий в соответствие функции f(z). определенной на L, аналитич. функцию… … Математическая энциклопедия
Вторая теорема разложения — Содержание 1 Теорема 2 Примеры 2.1 Случай простых полюсов … Википедия
ПЕРЕХОДНЫЙ ПРОЦЕСС — в электрическойцепи процесс установления нового режима в эле ктрич. цепи, возникающийв момент её коммутации. Коммутацией наз. любые скачкообразные переключенияпассивных элементов цепи, её ветвей или источников энергии. П. п. являетсяпромежуточным … Физическая энциклопедия
Интегральные преобразования — Одним из наиболее мощных средств решения дифференциальных уравнений, как обыкновенных, так, особенно, в частных производных, является метод интегральных преобразований. Преобразования Фурье, Лапласа, Ганкеля и другие применяются для решения задач … Википедия
 могла называться оригиналом, она должна удовлетворять трем условиям:
могла называться оригиналом, она должна удовлетворять трем условиям: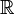 , притом на произвольном конечном интервале
, притом на произвольном конечном интервале  множество точек, в которых указанное условие не выполняется, конечно, притом в этих точках она должна претерпевать разрыв 1-го рода. Формально, для произвольного t, не относящегося к упомянутому множеству, должны существовать положительные постоянные
множество точек, в которых указанное условие не выполняется, конечно, притом в этих точках она должна претерпевать разрыв 1-го рода. Формально, для произвольного t, не относящегося к упомянутому множеству, должны существовать положительные постоянные  , такие, что
, такие, что  для произвольного
для произвольного ![h\in[-h_0;h_0]](/pictures/wiki/files/102/f13821f8f6d6aef162645b7aa925d203.png) .
. такие, что
такие, что  для произвольного
для произвольного  .
.