Определенный интеграл

Определенный интеграл
Определённый интеграл как площадь фигуры

В математическом анализе интегралом функции называют расширение понятия суммы. Процесс нахождения интеграла называется интегрированием. Этот процесс обычно используется при нахождений таких величин как площадь, объём, масса, смещение и т. д., когда задана скорость или распределение изменений этой величины по отношению к некоторой другой величине (положение, время и т. д.).


Существует несколько различных определений операции интегрирования, отличающиеся в технических деталях. Однако все они совместимы, то есть любые два способа интегрирования, если их можно применить к данной функции, дадут один и тот же результат.

Согласно основной теореме анализа, интегрирование — операция, обратная к дифференцированию.

Содержание

Типы интегралов

История

Знаки интеграла 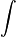\int и дифференцирования 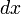~dx, были впервые использованы Лейбницем в конце XVII века. Символ интеграла образовался из буквы S — сокращения слова лат. summa (сумма).

Интеграл в древности

Интегрирование прослеживается ещё в древнем Египте, примерно в 1800 до н. э., Московский математический папирус демонстрирует знание формулы объёма усечённой пирамиды. Первым известным методом для расчёта интегралов является метод исчерпывания Евдокса (примерно 370 до н. э.), который пытался найти площади и объёмы, разрывая их на бесконечное множество частей, для которых площадь или объём уже известен. Этот метод был подхвачен и развит Архимедом, и использовался для расчёта площадей парабол и приближенного расчёта площади круга. Аналогичные методы были разработаны независимо в Китае в 3-м веке н.э Лю Хуэйем, который использовал их для нахождения площади круга. Этот метод был впоследствии использован Дзю Чонгши для нахождения объёма шара.

См. также

Ссылки



Wikimedia Foundation. 2010.

Игры ⚽ Поможем написать курсовую

Полезное


Смотреть что такое "Определенный интеграл" в других словарях:

  • ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ — (definite integral) Интеграл функции, вычисляемый на интервале, ограниченном верхним и нижним пределами. Если первой производной функции F(х) является f(x), то определенный интеграл f(x) равен F(x)+k. Определенный интеграл f(x) на интервале с… …   Экономический словарь

  • ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ — см. Интегральное исчисление …   Большой Энциклопедический словарь

  • ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ — см. Интеграл …   Математическая энциклопедия

  • ИНТЕГРАЛ — (integral) Функция, первая производная (first derivative) которой равна другой функции. Если f(х) является первой производной от g(x), то, следовательно, g(x) является интегралом f(х) и, таким образом, h(x)=g(x)+k, где k – произвольно выбранная… …   Экономический словарь

  • ИНТЕГРАЛ — (обозначение т ). Математический символ, используемый в ИСЧИСЛЕНИИ, представляющий операцию суммирования. Интеграл функции f(x), записанный как т f(x)dx, может представлять площадь фигуры, ограниченной кривой y=f(x) и осью абсцисс. ИНТЕГРИРОВАНИЕ …   Научно-технический энциклопедический словарь

  • Интеграл — Определённый интеграл как площадь фигуры У этого термина существуют и другие значения, см. Интеграл (значения). Интеграл функции  …   Википедия

  • ИНТЕГРАЛ — одно из центральных понятий математич. анализа и всей математики, возникновение к рого связано с двумя задачами: о восстановлении функции по ее производной (напр., с задачей об отыскании закона движения материальной точки вдоль прямой по… …   Математическая энциклопедия

  • интеграл — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] интеграл Есть два различных понятия — неопределенный И. и определенный И. Говорят, что функция f(x) имеет …   Справочник технического переводчика

  • интеграл Джоуля I2t — интеграл Джоуля Условная величина, характеризующая тепловое действие тока короткого замыкания на рассматриваемый элемент электроустановки, численно равная интегралу от квадрата тока короткого замыкания по времени, в пределах от начального момента …   Справочник технического переводчика

  • Интеграл — [integral]. Есть два различных понятия неопределенный И. и определенный И. Говорят, что функция f(x) имеет неопределенный И.  ∫f(x)dx, если существует такая функция F(x), что ее производная dF(x)/dx равна исходной функции f(x). Функция F(x)… …   Экономико-математический словарь


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»