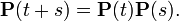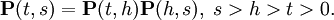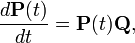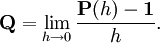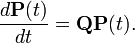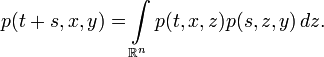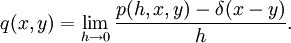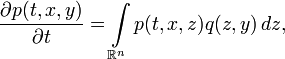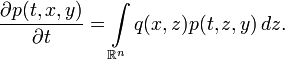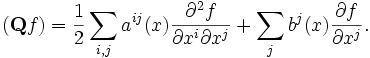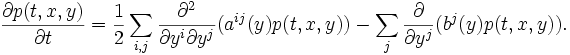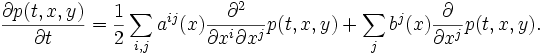Обратное уравнение Колмогорова

Уравнение Колмогорова — Чепмена для однопараметрического семейства непрерывных линейных операторов 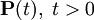$\mathbf{P}(t),\; t > 0$ в топологическом векторном пространстве выражает полугрупповое свойство:

$\mathbf{P}(t+s)=\mathbf{P}(t)\mathbf{P}(s).$

Чаще всего этот термин используется в теории однородных марковских случайных процессов, где 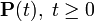$\mathbf{P}(t),\; t\geq 0$ — оператор, преобразующий распределение вероятностей в начальный момент времени в распределение вероятности в момент времени t ($\mathbf{P}(0)=\mathbf{1}$).

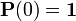Для неоднородных процессов рассматриваются двухпараметрические семейства операторов 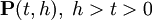$\mathbf{P}(t,h),\; h > t > 0$, преобразующих распределение вероятностей в момент времени t > 0 в распределение вероятности в момент времени h > t > 0. Для них уравнение Колмогорова—Чепмена имеет вид

$\mathbf{P}(t,s)=\mathbf{P}(t,h)\mathbf{P}(h,s), \;s > h > t > 0.$

Для систем с дискретным временем параметры t,h,s принимают натуральные значения.

Прямое и обратное уравнения Колмогорова

Формально дифференцируя уравнение Колмогорова—Чепмена по s при s = 0 получаем прямое уравнение Колмогорова:

$\frac{d \mathbf{P}(t)}{d t}=\mathbf{P}(t)\mathbf{Q},$

где

$\mathbf{Q}=\lim_{h \to 0}\frac{\mathbf{P}(h)-\mathbf{1}}{h}.$

Формально дифференцируя уравнение Колмогорова — Чепмена по t при t = 0 получаем обратное уравнение Колмогорова

$\frac{d \mathbf{P}(t)}{d t}=\mathbf{Q}\mathbf{P}(t).$

Необходимо подчеркнуть, что для бесконечномерных пространств оператор 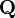$\mathbf{Q}$ уже не обязательно непрерывен, и может быть определен не всюду, например, быть дифференциальным оператором в пространстве распределений.

Примеры

Рассмотрим однородные марковские случайные процессы в 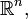$\mathbb{R}^n,$ для которых оператор переходных вероятностей 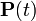$\mathbf{P}(t)$ задаётся переходной плотностью p(t,x,y): вероятность перехода из области U в область W за время t есть 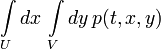$\int\limits_U dx \,\int\limits_V dy \, p(t,x,y)$. Уравнение Колмогорова—Чепмена для плотностей имеет вид:

$p(t+s,x,y)=\int\limits_{\mathbb{R}^n}p(t,x,z)p(s,z,y)\, dz .$

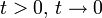При $t>0, \, t \to 0$ переходная плотность p(t,x,y) стремится к δ-функции (в смысле слабого предела обобщенных функций):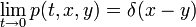$\lim_{t \to 0} p(t,x,y) = \delta(x-y)$. Это означает, что 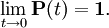$\lim_{t \to 0} \mathbf{P}(t)=\mathbf{1}.$ Пусть существует предел (также обобщённая функция)

$q(x,y)=\lim_{h \to 0}\frac{p(h,x,y)-\delta(x-y)}{h}.$

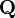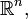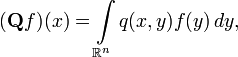Тогда оператор $\mathbf{Q}$ действует на функции f(x), определённые на $\mathbb{R}^n,$ как $(\mathbf{Q}f)(x) = \int\limits_{\mathbb{R}^n} q(x,y) f(y) \, dy ,$ и прямое уравнение Колмогорова принимает вид

$\frac{\partial p(t,x,y)}{\partial t}=\int\limits_{\mathbb{R}^n} p(t,x,z) q(z,y) \, dz,$

а обратное уравнение Колмогорова

$\frac{\partial p(t,x,y)}{\partial t}=\int\limits_{\mathbb{R}^n} q(x,z) p(t,z,y) \, dz .$

Пусть оператор 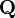$\mathbf{Q}$ — дифференциальный оператор второго порядка с непрерывными коэффициентами:

$(\mathbf{Q}f)= \frac{1}{2}\sum_{i,j} a^{ij}(x)\frac{\partial^2 f}{\partial x^i\partial x^j}+ \sum_j b^j(x) \frac{\partial f}{\partial x^j}.$

(это означает, что q(x,y) есть линейная комбинация первых и вторых производных δ(x − y) с непрерывными коэффициентами). Матрица a^ij симметрична. Пусть она положительно определена в каждой точке (диффузия). Прямое уравнение Колмогорова имеет вид

$\frac{\partial p(t,x,y)}{\partial t}= \frac{1}{2}\sum_{i,j} \frac{\partial^2}{\partial y^i\partial y^j}(a^{ij}(y)p(t,x,y))- \sum_j \frac{\partial }{\partial y^j}(b^j(y) p(t,x,y)).$

Это уравнение называется уравнением Фоккера — Планка. Вектор b^j в физической литературе называется вектором сноса, а матрица a^ij — тензором диффузии Обратное уравнение Колмогорова в этом случае

$\frac{\partial p(t,x,y)}{\partial t}= \frac{1}{2}\sum_{i,j} a^{ij}(x) \frac{\partial^2}{\partial x^i\partial x^j}p(t,x,y)+ \sum_j b^j(x) \frac{\partial }{\partial x^j} p(t,x,y).$

См. также

Цепь Маркова

Уравнение Фоккера — Планка

Литература

• Вентцель А. Д., Курс теории случайных процессов. — М.: Наука, 1996. — 400 с.