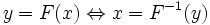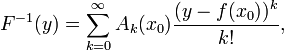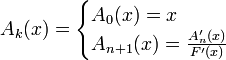- Обратное отображение
-
Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией.
Содержание
Определение
Функция
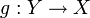 является обратной к функции
является обратной к функции 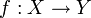 если для них выполнены следующие два тождества:
если для них выполнены следующие два тождества:- f(g(y)) = y для всякого
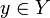
- g(f(x)) = x для всякого

Связанные определения
- Функция для которой существует обратная называется биекцией.
Существование
Чтобы найти обратную функцию, нужно решить уравнение x = F(y) относительно y. Если оно имеет более чем один корень, то функции обратной к F не существует.
Согласно теореме о неявной функции выразить y из уравнения x − F(y) = 0 возможно в том и только том случае, когда функция F(y) монотонна. Но даже в противном случае возможно обратить функцию на любом из промежутков её монотонности. Так, можно говорить, что
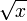 является обратной функцией к x2 на
является обратной функцией к x2 на 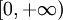 . На другом промежутке, точнее
. На другом промежутке, точнее ![(-\infty, 0]](/pictures/wiki/files/102/f9d75a40b8eadac31117745d2255ef61.png) , обратная функция другая:
, обратная функция другая: 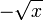 .
.Свойства
- Областью определения F − 1 является множество Y, а областью значений множество X.
- По построению имеем:
или
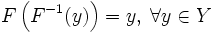 ,
,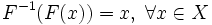 ,
,
или короче
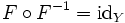 ,
,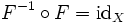 ,
,
где
 означает композицию функций, а idX,idY — тождественные отображения на X и Y соответственно.
означает композицию функций, а idX,idY — тождественные отображения на X и Y соответственно.- Функция F является обратной к F − 1:
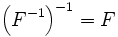 .
.
- Пусть
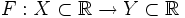 — биекция. Пусть
— биекция. Пусть 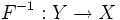 её обратная функция. Тогда графики функций y = F(x) и y = F − 1(x) симметричны относительно прямой y = x.
её обратная функция. Тогда графики функций y = F(x) и y = F − 1(x) симметричны относительно прямой y = x.
Степенной ряд
Обратная функция аналитической функции может быть представлена в виде степенного ряда:
где коэффициенты Ak задаются рекурсивной формулой:
Примеры
- Если
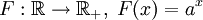 , где a > 0, то F − 1(x) = logax.
, где a > 0, то F − 1(x) = logax. - Если
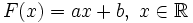 , где
, где 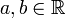 фиксированные постоянные, то
фиксированные постоянные, то 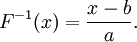
- Если
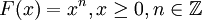 , то
, то ![F^{-1}(x)=\sqrt [n] {x}.](/pictures/wiki/files/48/0e8903e5e9bce2c5a76be6d025e20b9e.png)
См. также
- f(g(y)) = y для всякого
Wikimedia Foundation. 2010.